题目内容
 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
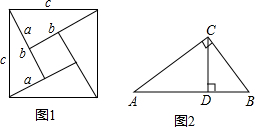
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=4,BC=3,求CD的长度.
分析:(1)根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式.
(2)先由勾股定理求出AB的长,再根据三角形的面积求CD的长即可.
(2)先由勾股定理求出AB的长,再根据三角形的面积求CD的长即可.
解答:解:(1)∵大正方形面积为c2,直角三角形面积为
ab,小正方形面积为:(b-a)2,
∴c2=4×
ab+(a-b)2=2ab+a2-2ab+b2
即c2=a2+b2.
(2)在Rt△ABC中,
∵∠ACB=90°,
∴由勾股定理,得:AB=
=
=5
∵CD⊥AB,
∴S△ABC=
AC•BC=
AB•CD
∴CD=
=
.
| 1 |
| 2 |
∴c2=4×
| 1 |
| 2 |
即c2=a2+b2.
(2)在Rt△ABC中,
∵∠ACB=90°,
∴由勾股定理,得:AB=
| AC2+BC2 |
| 42+32 |
∵CD⊥AB,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| 4×3 |
| 5 |
| 12 |
| 5 |
点评:本题考查了学生对勾股定理的证明和对三角形和正方形面积公式的熟练掌握和运用,属于基本题型.

练习册系列答案
相关题目


 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题: