题目内容
【题目】在平面直角坐标系中,某个函数图象上任意两点的坐标分别为(﹣t,y1)和(t,y2)(其中t为常数且t>0),将x<﹣t的部分沿直线y=y1翻折,翻折后的图象记为G1;将x>t的部分沿直线y=y2翻折,翻折后的图象记为G2,将G1和G2及原函数图象剩余的部分组成新的图象G.
例如:如图,当t=1时,原函数y=x,图象G所对应的函数关系式为y=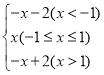 .
.
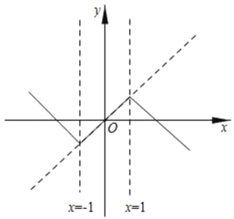
(1)当t=![]() 时,原函数为y=x+1,图象G与坐标轴的交点坐标是 .
时,原函数为y=x+1,图象G与坐标轴的交点坐标是 .
(2)当t=![]() 时,原函数为y=x2﹣2x
时,原函数为y=x2﹣2x
①图象G所对应的函数值y随x的增大而减小时,x的取值范围是 .
②图象G所对应的函数是否有最大值,如果有,请求出最大值;如果没有,请说明理由.
(3)对应函数y=x2﹣2nx+n2﹣3(n为常数).
①n=﹣1时,若图象G与直线y=2恰好有两个交点,求t的取值范围.
②当t=2时,若图象G在n2﹣2≤x≤n2﹣1上的函数值y随x的增大而减小,直接写出n的取值范围.
【答案】(1)(2,0);(2)①﹣![]() ≤x≤1或x≥
≤x≤1或x≥![]() ;②图象G所对应的函数有最大值为
;②图象G所对应的函数有最大值为![]() ;(3)①
;(3)①![]() ;②n≤
;②n≤![]() 或n≥
或n≥![]() .
.
【解析】
(1)根据题意分别求出翻转之后部分的表达式及自变量的取值范围,将y=0代入,求出x值,即可求出图象G与坐标轴的交点坐标;
(2)画出函数草图,求出翻转点和函数顶点的坐标,①根据图象的增减性可求出y随x的增大而减小时,x的取值范围,②根据图象很容易计算出函数最大值;
(3)①将n=﹣1代入到函数中求出原函数的表达式,计算y=2时,x的值.据(2)中的图象,函数与y=2恰好有两个交点时t大于右边交点的横坐标且-t大于左边交点的横坐标,据此求解.
②画出函数草图,分别计算函数左边的翻转点A,右边的翻转点C,函数的顶点B的横坐标(可用含n的代数式表示),根据函数草图以及题意列出关于n的不等式求解即可.
(1)当x=![]() 时,y=
时,y=![]() ,
,
当x≥![]() 时,翻折后函数的表达式为:y=﹣x+b,将点(
时,翻折后函数的表达式为:y=﹣x+b,将点(![]() ,
,![]() )坐标代入上式并解得:
)坐标代入上式并解得:
翻折后函数的表达式为:y=﹣x+2,
当y=0时,x=2,即函数与x轴交点坐标为:(2,0);
同理沿x=﹣![]() 翻折后当
翻折后当![]() 时函数的表达式为:y=﹣x,
时函数的表达式为:y=﹣x,
函数与x轴交点坐标为:(0,0),因为![]() 所以舍去.
所以舍去.
故答案为:(2,0);
(2)当t=![]() 时,由函数为y=x2﹣2x构建的新函数G的图象,如下图所示:
时,由函数为y=x2﹣2x构建的新函数G的图象,如下图所示:
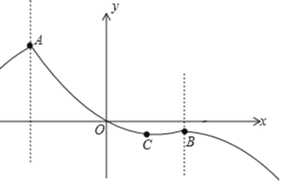
点A、B分别是t=﹣![]() 、t=
、t=![]() 的两个翻折点,点C是抛物线原顶点,
的两个翻折点,点C是抛物线原顶点,
则点A、B、C的横坐标分别为﹣![]() 、1、
、1、![]() ,
,
①函数值y随x的增大而减小时,﹣![]() ≤x≤1或x≥
≤x≤1或x≥![]() ,
,
故答案为:﹣![]() ≤x≤1或x≥
≤x≤1或x≥![]() ;
;
②函数在点A处取得最大值,
x=﹣![]() ,y=(﹣
,y=(﹣![]() )2﹣2×(﹣
)2﹣2×(﹣![]() )=
)=![]() ,
,
答:图象G所对应的函数有最大值为![]() ;
;
(3)n=﹣1时,y=x2+2x﹣2,
①参考(2)中的图象知:
当y=2时,y=x2+2x﹣2=2,
解得:x=﹣1±![]() ,
,
若图象G与直线y=2恰好有两个交点,则t>![]() ﹣1且-t>
﹣1且-t>![]() ,
,
所以![]() ;
;
②函数的对称轴为:x=n,
令y=x2﹣2nx+n2﹣3=0,则x=n±![]() ,
,
当t=2时,点A、B、C的横坐标分别为:﹣2,n,2,
当x=n在y轴左侧时,(n≤0),
此时原函数与x轴的交点坐标(n+![]() ,0)在x=2的左侧,如下图所示,
,0)在x=2的左侧,如下图所示,
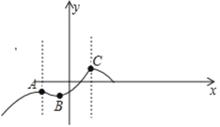
则函数在AB段和点C右侧,
故:﹣2≤x≤n,即:在﹣2≤n2﹣2≤x≤n2﹣1≤n,
解得:n≤![]() ;
;
当x=n在y轴右侧时,(n≥0),
同理可得:n≥![]() ;
;
综上:n≤![]() 或n≥
或n≥![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案