题目内容
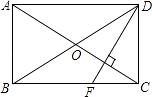
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
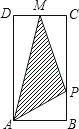
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.
【答案】
(1)
证明:如图①,
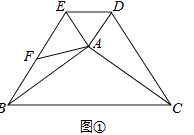
∵∠BAC+∠EAD=180°,∠BAE=90°,
∴∠DAC=90°,
在△ABE与△ACD中
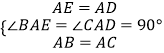
∴△ABE≌△ACD(SAS),
∴CD=BE,
∵在Rt△ABE中,F为BE的中点,
∴BE=2AF,
∴CD=2AF.
(2)
成立,
证明:如图②,
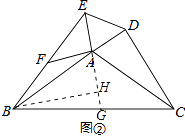
延长EA交BC于G,在AG上截取AH=AD,
∵∠BAC+∠EAD=180°,
∴∠EAB+∠DAC=180°,
∵∠EAB+∠BAH=180°,
∴∠DAC=∠BAH,
在△ABH与△ACD中,
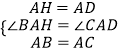
∴△ABH≌△ACD(SAS)
∴BH=DC,
∵AD=AE,AH=AD,
∴AE=AH,
∵EF=FB,
∴BH=2AF,
∴CD=2AF
【解析】(1)因为AF是直角三角形ABE的中线,所以BE=2AF,然后通过△ABE≌△ACD即可求得.(2)延长EA交BC于G,在AG上截取AH=AD,证出△ABH≌△ACD从而证得BH=CD,然后根据三角形的中位线等于底边的一半,求得BH=2AF,即可求得.

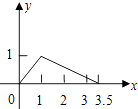
【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?