题目内容
求证:等腰三角形底边上的任意一点到两腰的距离之和等于一腰上的高.分析:根据三角形的面积公式S△=
底×高求得S△ABD、S△ACD、S△ABC;又由图易知,S△ABC=S△ABD+S△ACD,分析到这里,问题就迎刃而解了.
| 1 |
| 2 |
解答:已知:△ABC中,AB=AC,D为BC上任意一点,DE⊥AB,DF⊥AC,垂足为E、F,
CG⊥AB于G,
求证:CG=DE+DF.
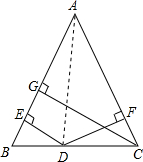 证明:已知如图所示.
证明:已知如图所示.
∵ED⊥AB,
∴S△ABD=
AB•ED;
∵DF⊥AC,
∴S△ACD=
AC•DF;
∵CG⊥AB,
∴S△ABC=
AB•CG;
又∵AB=AC,S△ABC=S△ABD+S△ACD,
∴
AB•CG=
AB•ED+
AC•DF,
∴CG=DE+DF.
CG⊥AB于G,
求证:CG=DE+DF.
 证明:已知如图所示.
证明:已知如图所示.∵ED⊥AB,
∴S△ABD=
| 1 |
| 2 |
∵DF⊥AC,
∴S△ACD=
| 1 |
| 2 |
∵CG⊥AB,
∴S△ABC=
| 1 |
| 2 |
又∵AB=AC,S△ABC=S△ABD+S△ACD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴CG=DE+DF.
点评:本题考查了等腰三角形的性质、三角形的面积公式等知识点;辅助线的作出是解答本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 下面两题任选一题
下面两题任选一题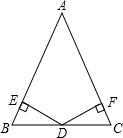 求证:等腰三角形底边上的中点到两腰的距离相等.结合所给图形,把“已知”、“求证”补充完整,并完成证明过程.
求证:等腰三角形底边上的中点到两腰的距离相等.结合所给图形,把“已知”、“求证”补充完整,并完成证明过程.