题目内容
 下面两题任选一题
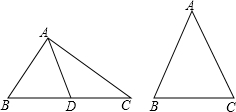
下面两题任选一题(1)求证:三角形一边上的中线小于另外两边之和的一半.
(2)求证:等腰三角形底边上任意一点到两腰的距离之和是一个定值.
分析:(1)延长AD到E,使AD=DE,连接BE,根据SAS判定△ACD≌△EBD,从而可得到BE=AC,再根据三角形三边关系即可证得结论;
(2)连接AD,根据等腰三角形的性质可表示出S△ABC=S△ABD+S△ACD的值,再根据S△ABC=
AB×AB边上的高,即可得到ED+FD=AB边上的高,即等腰三角形底边上任意一点到两腰的距离之和等于定值.
(2)连接AD,根据等腰三角形的性质可表示出S△ABC=S△ABD+S△ACD的值,再根据S△ABC=
| 1 |
| 2 |
解答: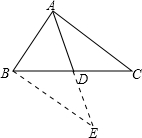 (1)证明:延长AD到E,使AD=DE,连接BE.
(1)证明:延长AD到E,使AD=DE,连接BE.
∵BD=DC,∠BDE=∠CDA,AD=DE,
∴△ACD≌△EBD,
∴BE=AC,
∵AB+BE>AE,AE=AD+DE=2AD,
∴AB+AC>2AD,
∴AD<
(AB+AC).
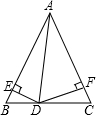
(2)证明:连接AD.
∵AB=AC
∴S△ABC=S△ABD+S△ACD=
AB×ED+
AC×FD=
×AB×(ED+FD)
∵S△ABC=
AB×AB边上的高
∴ED+FD=AB边上的高
∴等腰三角形底边上任意一点到两腰的距离之和等于定值.
 (1)证明:延长AD到E,使AD=DE,连接BE.
(1)证明:延长AD到E,使AD=DE,连接BE.∵BD=DC,∠BDE=∠CDA,AD=DE,
∴△ACD≌△EBD,
∴BE=AC,
∵AB+BE>AE,AE=AD+DE=2AD,
∴AB+AC>2AD,
∴AD<
| 1 |
| 2 |

(2)证明:连接AD.
∵AB=AC
∴S△ABC=S△ABD+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
∴ED+FD=AB边上的高
∴等腰三角形底边上任意一点到两腰的距离之和等于定值.
点评:此题主要考查等腰三角形的性质,三角形三边关系,全等三角形的判定与性质的综合运用.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目



 下面两题任选一题
下面两题任选一题