题目内容
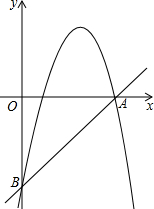 (2012•闸北区一模)已知:如图,直线y=x-15与x轴、y轴分别相交于点A和点B.抛物线y=-
(2012•闸北区一模)已知:如图,直线y=x-15与x轴、y轴分别相交于点A和点B.抛物线y=-| 1 | 3 |
(1)求这个抛物线的解析式;
(2)若这抛物线的顶点为点D,与x轴的另一个交点为点C.对称轴与x轴交于点H,求△DAC的面积;
(3)若点E是线段AD的中点.CE与DH交于点G,点P在y轴的正半轴上,△POH是否能够与△CGH相似?如果能,请求出点P的坐标;如果不能,请说明理由.
分析:(1)分别把x=0和y-0代入一次函数的解析式,求出A、B的坐标,代入抛物线得出方程组,求出方程组的解,即可得出抛物线的解析式;
(2)求出顶点D的坐标和C的坐标,根据三角形的面积公式求出即可;
(3)求出GH、HO、CH的值,根据相似三角形的性质得出两个比例式,代入即可求出P的坐标.
(2)求出顶点D的坐标和C的坐标,根据三角形的面积公式求出即可;
(3)求出GH、HO、CH的值,根据相似三角形的性质得出两个比例式,代入即可求出P的坐标.
解答:解:(1)∵y=x-15,
y=0时,0=x-15,
∴x=15,
当x=0时,y=-15,
∴A(15,0),B(0,-15),
代入得
,
解得
,
∴抛物线的解析式:y=-
x2+6x-15.
(2)抛物线的解析式可变形为y=-
(x-9)2+12,
∴顶点D坐标为(9,12),
设y=0,则-
(x-9)2+12=0,
∴(x-9)2=36.
∴x1=3,x2=15,
∴点C的坐标为(3,0),
∴S△DAC=
DH•AC=
×12×12=72.
(3)∵点E是线段AD的中点,点H是线段AC的中点,.
∴点G是△DAC的重心.如图: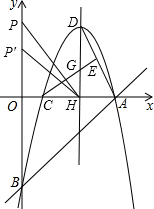
∵顶点D坐标为(9,12),
∴GH=
DH=4,
∴HO=9,CH=6.
设△POH∽△GHC时,
=
,
∴
=
∴PO=6,
∴P1(0,6);
△POH∽△CHG时,
=
,
=
,
∴PO=
.
∴P2(0,
).
∴△POH能够与△CHG相似,相似时点P的坐标为P1(0,6)或P2(0,
).
y=0时,0=x-15,
∴x=15,
当x=0时,y=-15,
∴A(15,0),B(0,-15),
代入得
|
解得
|
∴抛物线的解析式:y=-
| 1 |
| 3 |
(2)抛物线的解析式可变形为y=-
| 1 |
| 3 |
∴顶点D坐标为(9,12),
设y=0,则-
| 1 |
| 3 |
∴(x-9)2=36.
∴x1=3,x2=15,
∴点C的坐标为(3,0),
∴S△DAC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵点E是线段AD的中点,点H是线段AC的中点,.
∴点G是△DAC的重心.如图:

∵顶点D坐标为(9,12),
∴GH=
| 1 |
| 3 |
∴HO=9,CH=6.
设△POH∽△GHC时,
| PO |
| GH |
| HO |
| CH |
∴
| PO |
| 4 |
| 9 |
| 6 |
∴PO=6,
∴P1(0,6);
△POH∽△CHG时,
| PO |
| CH |
| HO |
| GH |
| PO |
| 6 |
| 9 |
| 4 |
∴PO=
| 27 |
| 2 |
∴P2(0,
| 27 |
| 2 |
∴△POH能够与△CHG相似,相似时点P的坐标为P1(0,6)或P2(0,
| 27 |
| 2 |
点评:本题考查了三角形的面积,用待定系数法求二次函数的解析式,二次函数图象上点的坐标,相似三角形的性质和判定等知识点的运用,主要培养了学生综合运用性质进行推理和计算的能力,题目比较典型,但有一定的难度,注意:分类讨论思想的运用.

练习册系列答案
相关题目