题目内容
【题目】如图，已知在 
中， 
， 
为 
边的中点，过点 作 
，垂足分别为 
．
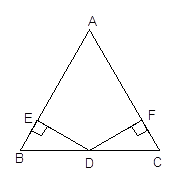
（1）求证： 
；
（2）若 
， 
= 
，求 的周长．
【答案】
（1）证明： 
，
，
，
.
是 
的中点，
.
(AAS)
（2）解： ， 
,
∴△ABC为等边三角形.
∴ 
，
，
∴ 
，
∴BE= 
BD，
，∴BD=2，∴BC=2BD=4，
∴ 
的周长为12．
【解析】（1）根据垂直的定义，可证得∠BED=∠CFD，再根据等边对等角去证明∠B=∠C ，根据线段中点的定义得出BD=CD，然后根据角角边证明△BED≌△CFD即可。
（2）根据有一个角是60°的等腰三角形是等边三角形，可证得△ABC为等边三角形，再根据30°角所对的直角边等于斜边的一半，求出BD的长，从而得到BC的长，即可求出△ABC的周长。
练习册系列答案
阅读快车系列答案
相关题目
【题目】已知二次函数y＝ax2＋bx＋c，其自变量x与函数y的对应值如下表：
x | … | －5 | －4 | －3 | －2 | －1 | 0 | … |
y | … | 4 | 0 | －2 | －2 | 0 | 4 | … |
则下列说法正确的是( )
A. 抛物线的开口向下 B. 当x＞－3时，y随x的增大而增大
C. 二次函数的最小值是－2 D. 抛物线的对称轴是直线x＝－
.