题目内容
 (1)如图在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°;求∠BAE和∠DAE的度数;
(1)如图在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°;求∠BAE和∠DAE的度数;(2)如果将条件“∠B=80°,∠C=40°”换成“∠B-∠C=50°”,你能得出∠DAE的度数吗?如果能,求出∠DAE的度数.
分析:(1)根据三角形的内角和定理求得∠BAC,再根据角平分线定义求得∠BAE即可;
(2)根据三角形的内角和定理、三角形的外角的性质以及角平分线定义,可以得出∠DAE和∠B-∠C的关系.
(2)根据三角形的内角和定理、三角形的外角的性质以及角平分线定义,可以得出∠DAE和∠B-∠C的关系.
解答:解:(1)∵∠B=80°,∠C=40°,AD⊥BC,
∴∠BAC=60°,∠CAD=50°.
又AE平分∠BAC,
∴∠BAE=∠CAE=30°,
∴∠DAE=20°.
(2)∵AD⊥BC,AE平分∠BAC,
∴∠DAE=90°-∠AED
=90°-(∠C+∠CAE)
=90°-(∠C+90°-
∠B-
∠C)
=
(∠B-∠C)
=25°.
∴∠BAC=60°,∠CAD=50°.
又AE平分∠BAC,
∴∠BAE=∠CAE=30°,
∴∠DAE=20°.
(2)∵AD⊥BC,AE平分∠BAC,
∴∠DAE=90°-∠AED
=90°-(∠C+∠CAE)
=90°-(∠C+90°-
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=25°.
点评:此题综合运用了三角形的内角和定理、三角形的外角的性质以及角平分线定义.

练习册系列答案
相关题目
 23、如图在△ABC中,D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于E,且∠EDC=50°,求∠A的度数.
23、如图在△ABC中,D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于E,且∠EDC=50°,求∠A的度数. 23、按要求完成作图,并回答问题;如图在△ABC中:
23、按要求完成作图,并回答问题;如图在△ABC中: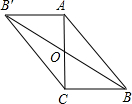 (2013•江西模拟)如图在ABC中,已知∠C=90°,AC=BC,BC=2,若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=( )
(2013•江西模拟)如图在ABC中,已知∠C=90°,AC=BC,BC=2,若以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,则BB′=( ) 如图在△ABC和△DEF中,AB=AC=DE=DF=5,BC=EF=6,移动△DEF,在整个移动过程中,点E始终在BC边上(点E不经过B、C两点),且DE经过点A,设EF与AC的交点为M.
如图在△ABC和△DEF中,AB=AC=DE=DF=5,BC=EF=6,移动△DEF,在整个移动过程中,点E始终在BC边上(点E不经过B、C两点),且DE经过点A,设EF与AC的交点为M. 如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F,AB=8,AC=6.则△ADE的周长=
如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F,AB=8,AC=6.则△ADE的周长=