题目内容
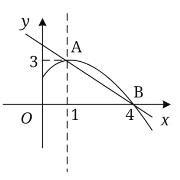
【题目】y=kx+b的图象经过点(﹣2,2)、(3,7)且与坐标轴相交于点、B两点.
(1)求一次函数的解析式.
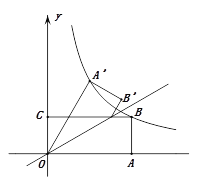
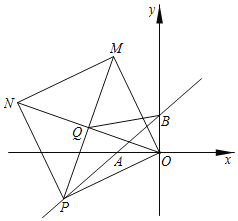
(2)如图,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,![]() 的值是否会发生变化?若不变,请求出其值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出其值;若变化,请说明理由.
(3)在(2)的条件下,在平面内有一点H,当以H、N、B、P为顶点的四边形为菱形时,直接写出点H的坐标.
【答案】(1)y=x+4;(2)![]() 的值不变,理由见解析;(3) 点H的坐标为
的值不变,理由见解析;(3) 点H的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法转化为解方程组解决问题.
(2)如图1中,结论:![]() 的值不变.连接BM,设PB交OM于G.想办法证明∠PBM=90°,利用直角三角形斜边中线的性质以及等腰直角三角形的性质即可解决问题.
的值不变.连接BM,设PB交OM于G.想办法证明∠PBM=90°,利用直角三角形斜边中线的性质以及等腰直角三角形的性质即可解决问题.
(3)分三种情形:如图2﹣1中,当四边形PBNH是菱形时,如图2﹣2中,当点P与A重合时.得到四边形PNMO是正方形(是菱形),此时H与原点O重合.如图2﹣3中,当四边形PBNH是菱形时,分别求解即可解决问题.
解:(1)∵y=kx+b的图象经过点(﹣2,2)、(3,7),
∴![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=x+4.
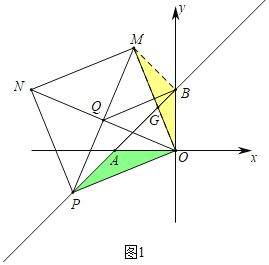
(2)如图1中,结论:![]() 的值不变.
的值不变.
理由:连接BM,设PB交OM于G.
∵直线y=x+4与坐标轴相交于点、B两点,
∴A(﹣4,0),B(0,4),
∴OA=OB=4,
∵四边形POMN是正方形,
∴∠POM=∠AOB=90°,OM=OP,
∴∠AOP=∠BOM,
∵OA=OB,
∴△AOP≌△BOM(SAS),
∴∠OPG=∠GMB,
∵∠OGP=∠BGM,
∴∠GBM=∠GOP=90°,
∴QM=QP,
∴QB=QP=QM,
∵△POQ是等腰直角三角形,
∴OP=![]() QP,
QP,
∴![]() .
.
(3)如图2﹣1中,当四边形PBNH是菱形时,
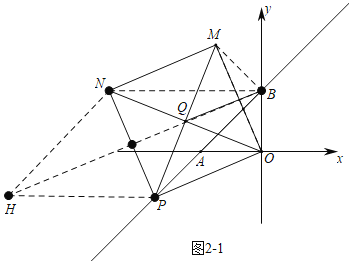
∵BH垂直平分线段PN,BH垂直平分线段OM,
∴BM=OB=4,
∴M(﹣2![]() ,4+2
,4+2![]() ),
),
∴P(﹣4﹣2![]() ,﹣2
,﹣2![]() ),
),
∴BN=BP=![]() ,
,
∴PH=BN=![]() ,
,
∵QB=QN=OQ,
∴∠NBO=90°,
∴BN∥OA∥PH,
∴H(﹣4﹣2![]() ,﹣2
,﹣2![]() ).
).
如图2﹣2中,当点P与A重合时,得到四边形PNMO是正方形(是菱形),此时H与原点O重合,H(0,0).

如图2﹣3中,当四边形PBNH是菱形时,设PH交OB于J,在JO上取一点F,使得PJ=JF.
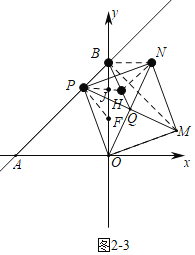
∵BP=BN,
∴∠BPN=∠BNP=22.5°,
∵∠OPN=90°,∠PAO=45°,
∴∠APO=67.5°,
∴∠AOP=67.5°,
∴∠POJ=22.5°,
∵∠PFJ=∠FPO+∠POF=45°,
∴∠FPO=∠POF=22.5°,
∴PF=OF,设PJ=BJ=JF=x,则PB=BN=PF=OF=![]() x,
x,
∴2x+![]() x=4,
x=4,
∴x=4﹣2![]() ,
,
∴BN=PH=4![]() ﹣4,P(2
﹣4,P(2![]() ﹣4,2
﹣4,2![]() ),
),
∴H(6![]() ﹣8,2
﹣8,2![]() ),
),
综上所述,满足条件的点H的坐标为(﹣4﹣2![]() ﹣4
﹣4![]() ,﹣2
,﹣2![]() )或(0,0)或(6
)或(0,0)或(6![]() ﹣8,2
﹣8,2![]() ).
).

 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案