题目内容
如图,已知抛物线y=x2+bx+c过点A(3,0)和原点O.正方形BCDE的顶点B在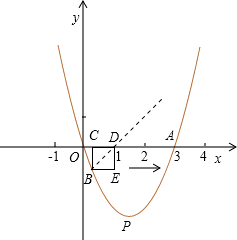 抛物线y=x2+bx+c上,且在对称轴的左侧,点C、D在x轴上,点E在第四象限,且OD=1.
抛物线y=x2+bx+c上,且在对称轴的左侧,点C、D在x轴上,点E在第四象限,且OD=1.
(1)求这条抛物线的解析式.
(2)求正方形BCDE的边长.
(3)若正方形BCDE沿x轴向右平移,当正方形的顶点落在抛物线y=x2+bx+c上时,求平移的距离.
解:(1)由题意可得: ,
,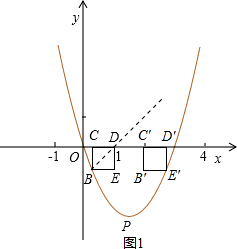
解得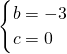 .
.
故这条抛物线的解析式y=x2-3x.
(2)设正方形的边长为a,
∵OD=1,
∴OD=1-a,
∴B(1-a,-a)代入解析式:-a=(1-a)2-3(1-a).
解得:a1= -1,a2=-1-
-1,a2=-1- (不合题意舍去),
(不合题意舍去),
故正方形BCDE的边长为: -1;
-1;
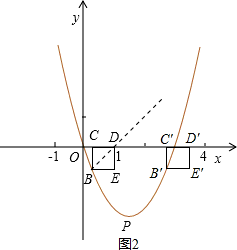 (3)①当E点运动到抛物线上时,设平移后正方形为B′C′D′E′,
(3)①当E点运动到抛物线上时,设平移后正方形为B′C′D′E′,
根据抛物线的对称性可知:E′(1+ ,1-
,1- ),
),
因此OD′=1+ ,即平移的距离为OD′-OD=
,即平移的距离为OD′-OD= .
.
②当B点运动到抛物线上时,同理可求得B′(1+ ,1-
,1- ),
),
因此OC′=1+ ,
,
因为OC=1-a=2- ,
,
因此平移的距离为OC′-OC=2 -1.
-1.
③当D点运动到抛物线上时,可得D′(3,0),因此平移的距离为OD′-OD=3-1=2.
④当C点运动到抛物线上时,可得C′(3,0),因此抛物线移动的距离为OC′-OC=3-(2- )=1+
)=1+ .
.
综上所述,正方形平移的距离为 ,2,2
,2,2 -1,
-1, +1.
+1.
分析:(1)将A和原点的坐标代入抛物线中,即可求出抛物线的解析式.
(2)可设出C的坐标如(a,0),那么CD=BC=1-a,因此B点坐标为(a,1-a)代入抛物线的解析式中即可求出B点坐标,代入求得的函数解析式即可求得a值,从而求得正方形的边长.
(3)本题要按四边顶点分别在抛物线的图象上这四种情况进行求解,解题思路一致.以E点落在抛物线图象上为例说明:题(2)已经求出了正方形的边长为 -1,根据抛物线的对称性,那么此时E′的坐标为(1+
-1,根据抛物线的对称性,那么此时E′的坐标为(1+ ,1-
,1- ),已知了OD=6,而OD′=1+
),已知了OD=6,而OD′=1+ ,因此移动的距离为OD′-OD=
,因此移动的距离为OD′-OD= ..
..
点评:本题考查了二次函数解析式的确定、正方形的性质、函数图象的平移、一次函数的应用等知识,考查的知识点比较多,题目难度比较大.
 ,
,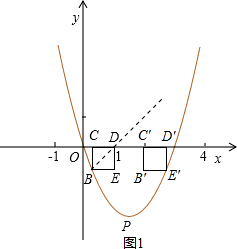
解得
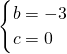 .
.故这条抛物线的解析式y=x2-3x.
(2)设正方形的边长为a,
∵OD=1,
∴OD=1-a,
∴B(1-a,-a)代入解析式:-a=(1-a)2-3(1-a).
解得:a1=
 -1,a2=-1-
-1,a2=-1- (不合题意舍去),
(不合题意舍去),故正方形BCDE的边长为:
 -1;
-1;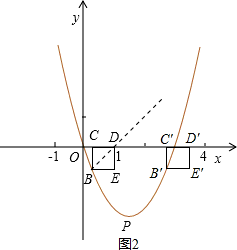 (3)①当E点运动到抛物线上时,设平移后正方形为B′C′D′E′,
(3)①当E点运动到抛物线上时,设平移后正方形为B′C′D′E′,根据抛物线的对称性可知:E′(1+
 ,1-
,1- ),
),因此OD′=1+
 ,即平移的距离为OD′-OD=
,即平移的距离为OD′-OD= .
.②当B点运动到抛物线上时,同理可求得B′(1+
 ,1-
,1- ),
),因此OC′=1+
 ,
,因为OC=1-a=2-
 ,
,因此平移的距离为OC′-OC=2
 -1.
-1.③当D点运动到抛物线上时,可得D′(3,0),因此平移的距离为OD′-OD=3-1=2.
④当C点运动到抛物线上时,可得C′(3,0),因此抛物线移动的距离为OC′-OC=3-(2-
 )=1+
)=1+ .
.综上所述,正方形平移的距离为
 ,2,2
,2,2 -1,
-1, +1.
+1.分析:(1)将A和原点的坐标代入抛物线中,即可求出抛物线的解析式.
(2)可设出C的坐标如(a,0),那么CD=BC=1-a,因此B点坐标为(a,1-a)代入抛物线的解析式中即可求出B点坐标,代入求得的函数解析式即可求得a值,从而求得正方形的边长.
(3)本题要按四边顶点分别在抛物线的图象上这四种情况进行求解,解题思路一致.以E点落在抛物线图象上为例说明:题(2)已经求出了正方形的边长为
 -1,根据抛物线的对称性,那么此时E′的坐标为(1+
-1,根据抛物线的对称性,那么此时E′的坐标为(1+ ,1-
,1- ),已知了OD=6,而OD′=1+
),已知了OD=6,而OD′=1+ ,因此移动的距离为OD′-OD=
,因此移动的距离为OD′-OD= ..
..点评:本题考查了二次函数解析式的确定、正方形的性质、函数图象的平移、一次函数的应用等知识,考查的知识点比较多,题目难度比较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;