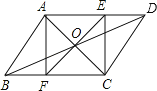
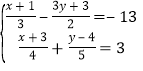题目内容
【题目】如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
(1)求证:四边形PMEN是平行四边形;
(2)请直接写出当AP为何值时,四边形PMEN是菱形;
(3)四边形PMEN有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.

【答案】(1)证明见解析(2)四边形PMEN是菱形;(3)当AP=2或AP=8时,四边形PMEN是矩形
【解析】试题分析:
⑴根据三角形的中位线的性质和平行四边形的判定定理即可证明.
⑵当DP=CP时,四边形PMEN是菱形,P是AB的中点,所以可求出AP的值.
⑶四边形PMEN是矩形的话,∠DPC必须为90°,那么判断一下△DPC是不是直角三角形即可.
试题解析:
(1)∵ M、N、E分别是PD、PC、CD的中点,
∴ ME是PC的中位线,NE是PD的中位线,
∴ ME∥PC,EN∥PD,
∴ 四边形PMEN是平行四边形;
(2)当AP=5时,
在Rt△ PAD和Rt△ PBC中,
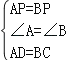 ,
,
∴ △ PAD≌ △ PBC,
∴ PD=PC,
∵ M、N、E分别是PD、PC、CD的中点,
∴ NE=PM=![]() PD,ME=PN=
PD,ME=PN=![]() PC,
PC,
∴ PM=ME=EN=PN,
∴ 四边形PMEN是菱形;
(3)四边形PMEN可能是矩形.
若四边形PMEN是矩形,则∠ DPC=90°.
设PA=x,PB=10﹣x,
DP=![]() ,CP=
,CP=![]() .
.
DP2+CP2=DC2
16+x2+16+(10﹣x)2=102
x2﹣10x+16=0
x=2或x=8.
故当AP=2或AP=8时,四边形PMEN是矩形.

【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?