题目内容
已知抛物线y=ax2+bx+c(a<0)与x轴交于A、B两点,点A在x轴的负半轴上,点B在x轴的正半轴上,又此抛物线交y轴于点C,连AC、BC,且满足△OAC的面积与△OBC的面积之差等于两线段OA与OB的积(即S△OAC-S△OBC=OA•OB)(1)求b的值;
(2)若tan∠CAB=
| 1 |
| 2 |
| 13 |
| 4 |
分析:(1)可根据S△OAC-S△OBC=OA•OB来求解,先用OA、OC、OB的长,表示出△OAC、△OBC的面积,然后根据韦达定理即可求出b的值.
(2)先根据tan∠CAB的值,在直角三角形AOC中,用OC表示出OA的长,即可得出A点的坐标,将A的坐标代入抛物线的解析式中,可将抛物线解析式中的待定系数减少为1个,然后用这个待定系数表示出P、B点的坐标,即可得出AB的长,如果过P作抛物线的对称轴交x轴于M,交圆于N,那么△PAB的外心必在PN(抛物线的对称轴)上,那么可根据相交弦定理得出AM•BM=PM•MN,据此可求出抛物线中的待定系数,由此可得出抛物线的解析式.
(2)先根据tan∠CAB的值,在直角三角形AOC中,用OC表示出OA的长,即可得出A点的坐标,将A的坐标代入抛物线的解析式中,可将抛物线解析式中的待定系数减少为1个,然后用这个待定系数表示出P、B点的坐标,即可得出AB的长,如果过P作抛物线的对称轴交x轴于M,交圆于N,那么△PAB的外心必在PN(抛物线的对称轴)上,那么可根据相交弦定理得出AM•BM=PM•MN,据此可求出抛物线中的待定系数,由此可得出抛物线的解析式.
解答: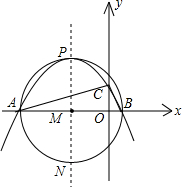 解:(1)设A(x1,0)、B(x2,0),由题设可求得C点的坐标为(0,c)
解:(1)设A(x1,0)、B(x2,0),由题设可求得C点的坐标为(0,c)
且x1<0,x2>0
∵a<0,
∴c>0
由S△AOC-S△BOC=OA×OB
得:-
x1c-
x2c=-x1x2
得:
c(-
)=
得:b=-2
(2)设抛物线的对称轴与x轴交于点M,与△PAB的外接圆交于点N
∵tan∠CAB=
∴OA=2•OC=2c
∴A点的坐标为(-2c,0)
∵A点在抛物线上,
∴x=-2c,
y=0代入y=ax2-2x+c
得a=-
又∵x1、x2为方程ax2-2x+c=0的两根
∴x1+x2=-
=
即-2c+x2=
=-
c
∴x2=
c
∴B点的坐标为(
c,0)
∴顶点P的坐标为(-
c,
c)
由相交弦定理得:AM•BM=PM•MN
又∵AB=
c,
∴AM=BM=
c,PM=
c
∴(
c)2=
c(
-
c)
∴c=
,a=-
(9分)
∴所求抛物线的函数解析式是:y=-
x2-2x+
.
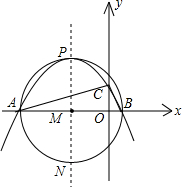 解:(1)设A(x1,0)、B(x2,0),由题设可求得C点的坐标为(0,c)
解:(1)设A(x1,0)、B(x2,0),由题设可求得C点的坐标为(0,c)且x1<0,x2>0
∵a<0,
∴c>0
由S△AOC-S△BOC=OA×OB
得:-
| 1 |
| 2 |
| 1 |
| 2 |
得:
| 1 |
| 2 |
| b |
| a |
| c |
| a |
得:b=-2
(2)设抛物线的对称轴与x轴交于点M,与△PAB的外接圆交于点N
∵tan∠CAB=
| 1 |
| 2 |
∴OA=2•OC=2c
∴A点的坐标为(-2c,0)
∵A点在抛物线上,
∴x=-2c,
y=0代入y=ax2-2x+c
得a=-
| 5 |
| 4c |
又∵x1、x2为方程ax2-2x+c=0的两根
∴x1+x2=-
| b |
| a |
| 2 |
| a |
即-2c+x2=
| 2 |
| a |
| 8 |
| 5 |
∴x2=
| 2 |
| 5 |
∴B点的坐标为(
| 2 |
| 5 |
∴顶点P的坐标为(-
| 4 |
| 5 |
| 9 |
| 5 |
由相交弦定理得:AM•BM=PM•MN
又∵AB=
| 12 |
| 5 |
∴AM=BM=
| 6 |
| 5 |
| 9 |
| 5 |
∴(
| 6 |
| 5 |
| 9 |
| 5 |
| 13 |
| 2 |
| 9 |
| 5 |
∴c=
| 5 |
| 2 |
| 1 |
| 2 |
∴所求抛物线的函数解析式是:y=-
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了二次函数解析式的确定,韦达定理,相交弦定理等知识点.综合性较强,考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=