题目内容
 如图,边长为2cm的正六边形ABCDEF的中心在坐标原点上,点B在x轴的负半轴上.
如图,边长为2cm的正六边形ABCDEF的中心在坐标原点上,点B在x轴的负半轴上.
(1)求出点A、点D、点E的坐标;
(2)求出图象过A、D、E三点的二次函数的解析式.
 解:(1)设AF与y轴交于点G,连接OA,过点A作AH⊥x轴,垂足为H;
解:(1)设AF与y轴交于点G,连接OA,过点A作AH⊥x轴,垂足为H;由已知AF=2,得AG=1,AH=
 ,∠AOH=60°(正六边形的性质),
,∠AOH=60°(正六边形的性质),∴A(-1,
 );
);同理D(1,-
 ),E(2,0);
),E(2,0);(2)设所求二次函数解析式为y=ax2+bx+c;
由(1)知,函数图象过(-1,
 )、(1,-
)、(1,- )、(2,0)三点,得:
)、(2,0)三点,得: ,
,解此方程组,得
 ;
;因此所求二次函数解析式是y=
 x2-
x2- x-
x- .
.分析:(1)连接OA,过A作x轴的垂线,设垂足为H;易知AG=OH=1,在Rt△AOH中,由正六边形的性质可得∠AOH=60°,通过解直角三角形即可求得AH的长,也就得到了A点的坐标;同理可求得E、D的坐标;
(2)用待定系数法即可求得过A、D、E的二次函数解析式.
点评:此题主要考查了正六边形的性质及二次函数解析式的确定等知识.

练习册系列答案
相关题目
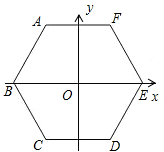 如图,边长为2cm的正六边形ABCDEF的中心在坐标原点上,点B在x轴的负半轴上.
如图,边长为2cm的正六边形ABCDEF的中心在坐标原点上,点B在x轴的负半轴上. 25、如图,边长为2cm的正方形剪成四个全等的直角三角形,请将四个直角三角形拼成符合下列要求的图形(全部用上,互不重叠,且不留空隙,).
25、如图,边长为2cm的正方形剪成四个全等的直角三角形,请将四个直角三角形拼成符合下列要求的图形(全部用上,互不重叠,且不留空隙,).
