题目内容
【题目】某中学计划从办公用品公司购买A,B两种型号的小黑板.经洽谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需多少元.
(2)根据该中学实际情况,需从公司购买A,B两种型号的小黑板共60块,要求购买A,B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的 ![]() .则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
【答案】
(1)解:设一块A型小黑板x元,一块B型小黑板y元.
则 ![]() ,
,
解得 ![]() .
.
答:一块A型小黑板100元,一块B型小黑板80元
(2)解:设购买A型小黑板m块,则购买B型小黑板(60﹣m)块
则 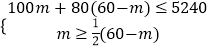 ,
,
解得20≤m≤22,
又∵m为正整数
∴m=20,21,22
则相应的60﹣m=40,39,38
∴共有三种购买方案,分别是
方案一:购买A型小黑板20块,购买B型小黑板40块;
方案二:购买A型小黑板21块,购买B型小黑板39块;
方案三:购买A型小黑板22块,购买B型小黑板38块.
方案一费用为100×20+80×40=5200元;
方案二费用为100×21+80×39=5220元;
方案三费用为100×22+80×38=5240元.
∴方案一的总费用最低,
即购买A型小黑板20块,购买B型小黑板40块总费用最低,为5200元
【解析】(1)设购买一块A型小黑板需要x元,一块B型为y元,根据等量关系:购买一块A型小黑板比买一块B型小黑板多用20元;购买5块A型小黑板和4块B型小黑板共需820元;可列方程组求解.(2)设购买A型小黑板m块,则购买B型小黑板(60﹣m)块,根据需从公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的 ![]() ,可列不等式组求解.
,可列不等式组求解.
【考点精析】关于本题考查的一元一次不等式组的应用,需要了解1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能得出正确答案.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案