Question

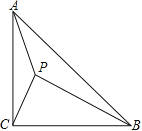
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝5cm，∠BAC＝60°，动点M从点B出发，在BA边上以2cm/s的速度向点A匀速运动，同时动点N从点C出发，在CB边上以cm/s的速度向点B匀速运动，设运动时间为ts（0≤t≤5），连接MN．

发现：BM＝　 　cm，BN＝　 　cm；（用含t的式子来表示）

猜想：（1）若BM＝BN，求t值；

（2）若△MBN与△ABC相似，求t值．

探究：是否存在符合条件的t，使△BMN与四边形AMNC面积相等？若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】发现：BM＝2tcm，BN＝cm；猜想：（1）t＝（10﹣15）秒；（2）或秒；探究：不存在时间t，使△BMN与四边形AMNC面积相等，理由详见解析．

【解析】

发现：利用路程等于速度乘以时间即可得出结论；

猜想：（1）利用BM＝BN建立方程求解即可得出结论；

（2）分两种情况，利用相似三角形得出比例式建立方程求解即可得出结论；

探究：先求出△ABC的面积，进而求出△BMN的面积，最后用△BMN的面积建立方程，判断出此方程无解，即可得出结论．

解：发现：在Rt△ABC中，∠BAC＝60°，

∴∠B＝30°，

∵AC＝5cm，

∴AB＝2AC＝10cm，BC=AC＝5cm，

由运动知，BM＝2t（cm），CN＝t（cm），

∴BN＝BC﹣CN＝5﹣t（cm），

故答案为：2t，（5﹣t）；

猜想：（1）∵BM＝BN，

∴2t＝5﹣t，

∴t＝（10﹣15）秒；

（2）∵△MBN与△ABC相似，

①当△MBN∽△ABC时，∴ ，

∴ ，

∴t＝ 秒，

②当△MBN∽△CBA时，∴，

∴，

∴t＝秒，

即：满足条件的t的值为或秒；

探究：∵AC＝5，BC＝5 ，

∴S△ABC＝ACBC＝cm2，

∵△BMN与四边形AMNC面积相等，

∴S△BMN＝S△ABC＝cm2，

如图，过点M作MD⊥BC于D，

在Rt△BDM中，∠B＝30°，BM＝2t，

∴DM＝BM＝t，

∴S△BMN＝BNDM＝（5 ﹣t）t＝，

∴2t2﹣10t+25＝0，

而△＝102﹣4×2×25＝100﹣200＝﹣100＜0，

∴此方程无解，

即：不存在时间t，使△BMN与四边形AMNC面积相等．