题目内容
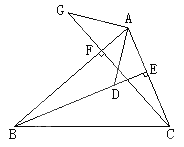
【题目】如图，将△ABC沿它的中位线MN折叠后，点A落在点A′处，若∠A=30°，∠B=115°，则∠A′NC=°．
【答案】110
【解析】解：∵∠A=30°，∠B=115°，
∴∠C=180°﹣∠A﹣∠B=180°﹣30°﹣115°=35°，
∵MN是三角形的中位线，
∴MN∥BC，
∴∠A′NM=∠C=35°，∠CNM=180°﹣∠C=180°﹣35°=145°，
∴∠A′NC=∠CNM﹣∠A′NM=145°﹣35°=110°．
所以答案是：110．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
