Question

【题目】求证：三角形的内角和等于.

(要求，画图，据图写出已知，求证，证明)

Answer 1

【答案】见解析

【解析】

首先根据题意，写出本题的已知条件与求证内容，然后过点A作EF∥BC；已知EF∥BC，根据两直线平行，内错角相等，可得∠FAC=∠C，∠EAB=∠∠B；再根据E、A、F三点共线，可得∠EAB+∠BAC+∠FAC=180°，结合以上所得结论，即可求证本题.

已知△ABC，求证：∠CBA+∠BAC+∠ACB=180°.

证明：根据题意画出简单示意图，过点A作EF∥BC.

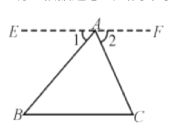
∵EF∥BC，

∴∠CAF=∠ACB，∠EAB=∠CBA.

∵∠CAF=∠ACB，∠EAB=∠CBA，∠EAB+∠BAC+∠CAF=180°，

∴∠CBA+∠BAC+∠ACB=180°，即三角形的内角和等于180°