��Ŀ����
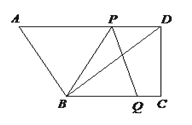
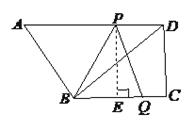
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����C��90�㣬BC��8��DC��6��AD��10.����P�ӵ�D���������߶�DA�ķ�����ÿ��2����λ�����ٶ��˶�������Q�ӵ�C���������߶�CB����ÿ��1����λ�����ٶ����B�˶�����P��Q�ֱ�ӵ�D��Cͬʱ����������P�˶�����Aʱ����Q��ֹ֮ͣ�˶�.���˶���ʱ��Ϊt���룩
(1)���ı���ABQPΪƽ���ı���,���˶�ʱ��t.
��2����tΪ��ֵʱ��������BPQ����BQ��BPΪ�ױߵĵ��������Σ�
���𰸡���1��t��2����2��![]() ��
��![]()
�������������������1�����ı���ABQPΪƽ���ı���ʱ��AP=BQ����21-2t=16-t���ɽ�t�����
��2������Ӧ����������������ۣ�����PQ=BQ����Rt��PQM�У���PQ2=PM2+MQ2��PQ=QB���������ݴ��룬�ɽ�ʱ��t�����
����PB=PQ��PB2=PM2+BM2��PB=PQ�������ݴ��룬�ɽ�ʱ��t�����
���������(1) ���ı���ABQPΪƽ���ı���,
��AP=BQ,
��![]()
![]()
![]()
![]()
��2���١�QΪ����ʱ��QB=QP��
�� ![]() ��
��
��� ![]()
�ڡ�PΪ����ʱ��PB=PQ���У� ![]() ��
��
��� ![]() ��
��
���ϣ� ![]() ��
��![]() ʱ����������.
ʱ����������.

��ϰ��ϵ�д�
 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
�����Ŀ