题目内容
 如图,BC是⊙O的弦,OD⊥BC于E,交
如图,BC是⊙O的弦,OD⊥BC于E,交 |
| BC |
| 3 |
(1)求⊙O的半径;
(2)求图中阴影部分面积的最大值.
分析:(1)连接OB,利用垂径定理易得BE的长,在Rt△OBE中,设半径为R,利用勾股定理得到关于R的方程,解方程即可求得半径长;
(2)当点A最高即AD为直径时阴影部分面积的最大值,利用OB=4,OE=4-2=2得∠OBE=30°,则∠BOD=60°,根据三角形的面积公式和扇形的面积公式可计算出等边△OBD的面积、扇形OBD的面积,则可得到弓形BD的面积,然后利用阴影部分面积的最大值=△ABD的面积+弓形BD的面积计算即可.
(2)当点A最高即AD为直径时阴影部分面积的最大值,利用OB=4,OE=4-2=2得∠OBE=30°,则∠BOD=60°,根据三角形的面积公式和扇形的面积公式可计算出等边△OBD的面积、扇形OBD的面积,则可得到弓形BD的面积,然后利用阴影部分面积的最大值=△ABD的面积+弓形BD的面积计算即可.
解答:解:(1)连OB,如图,
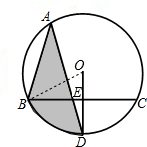 ∵OD⊥BC,
∵OD⊥BC,
∴BE=
BC=
×4
=2
,
设⊙O的半径为R,则OE=R-DE=R-2,
在Rt△OEB中,OB2=OE2+BE2,即R2=(2
)2+(R-2)2,
∴R=4;
(2)如图∵弓形BD的面积不变,当△ABD的面积最大时,阴影部分的面积最大,
即点AD在线段BD的中垂线上时阴影部分面积的最大值,
∵OB=4,OE=4-2=2,
∴∠OBE=30°,
∴∠BOD=60°,
可求出此时BD边上的高为:4+2
,
∴SABD=
×4×(4+2
)=8+4
,
∴等边△OBD的面积=
×42=4
,
∵扇形OBD的面积=
=
π,
∴弓形BD的面积=
π-4
,
∴阴影部分面积的最大值=△ABD的面积+弓形BD的面积=8+4
-4
+
π=8+
π.
 ∵OD⊥BC,
∵OD⊥BC,∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
设⊙O的半径为R,则OE=R-DE=R-2,
在Rt△OEB中,OB2=OE2+BE2,即R2=(2
| 3 |
∴R=4;
(2)如图∵弓形BD的面积不变,当△ABD的面积最大时,阴影部分的面积最大,
即点AD在线段BD的中垂线上时阴影部分面积的最大值,
∵OB=4,OE=4-2=2,
∴∠OBE=30°,
∴∠BOD=60°,
可求出此时BD边上的高为:4+2
| 3 |
∴SABD=
| 1 |
| 2 |
| 3 |
| 3 |
∴等边△OBD的面积=
| ||
| 4 |
| 3 |
∵扇形OBD的面积=
| 60•π•42 |
| 360 |
| 8 |
| 3 |
∴弓形BD的面积=
| 8 |
| 3 |
| 3 |
∴阴影部分面积的最大值=△ABD的面积+弓形BD的面积=8+4
| 3 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理以及扇形的面积公式.

练习册系列答案
相关题目
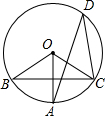 如图,BC是⊙O的弦,OA⊥BC,∠AOB=70°,则∠ADC的度数是( )
如图,BC是⊙O的弦,OA⊥BC,∠AOB=70°,则∠ADC的度数是( )| A、70° | B、35° | C、45° | D、60° |
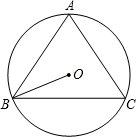 已知:如图,BC是⊙O的弦,点A在⊙O上,AB=AC=10,
已知:如图,BC是⊙O的弦,点A在⊙O上,AB=AC=10, 17、如图,BC是⊙O的弦,圆周角∠BAC=50°,则∠OCB的度数是
17、如图,BC是⊙O的弦,圆周角∠BAC=50°,则∠OCB的度数是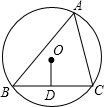 如图,BC是⊙O的弦,A是⊙O上一点,OD⊥BC于D,且BD=
如图,BC是⊙O的弦,A是⊙O上一点,OD⊥BC于D,且BD=