题目内容
在实数0, ,-
,- ,0、74,π中,无理数有________个;从2,-2,1,-1四个数中任取2个数求和,其和为0的概率是________;顺次连接等腰梯形各边中点所成的四边形是________.
,0、74,π中,无理数有________个;从2,-2,1,-1四个数中任取2个数求和,其和为0的概率是________;顺次连接等腰梯形各边中点所成的四边形是________.
2  菱形
菱形
分析:根据无理数的概念对各个数进行分析,从而可得到答案;
根据列表法进行分析看符合条件的个数占总个数的比例;
根据等腰梯形的性质和三角形中位线定理进行分析,从而可得到答案.
解答:由无理数的概念得,题中的无理数有: ,π,共两个;
,π,共两个;
四个数中两数之和为零的有两组,所以其概率=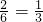 ;
;
根据等腰梯形的性质可知其两对角线相等,根据中位线定理可得其各边的中点组成的四边形是菱形.
点评:此题考查学生对无理数的概念等腰梯形的性质等知识点的综合运用.用到的知识点为:概率=所求情况数与总情况数之比.顺次连接对角线相等的四边形的中点得到的四边形是菱形.
 菱形
菱形分析:根据无理数的概念对各个数进行分析,从而可得到答案;
根据列表法进行分析看符合条件的个数占总个数的比例;
根据等腰梯形的性质和三角形中位线定理进行分析,从而可得到答案.
解答:由无理数的概念得,题中的无理数有:
 ,π,共两个;
,π,共两个;四个数中两数之和为零的有两组,所以其概率=
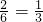 ;
;根据等腰梯形的性质可知其两对角线相等,根据中位线定理可得其各边的中点组成的四边形是菱形.
点评:此题考查学生对无理数的概念等腰梯形的性质等知识点的综合运用.用到的知识点为:概率=所求情况数与总情况数之比.顺次连接对角线相等的四边形的中点得到的四边形是菱形.

练习册系列答案
相关题目
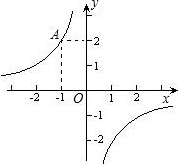 如图,在平面直角坐标系中点A在反比例函数图象上,一条抛物线的顶点是(1,2)且过点(2,3),解答下列问题.
如图,在平面直角坐标系中点A在反比例函数图象上,一条抛物线的顶点是(1,2)且过点(2,3),解答下列问题.