题目内容
已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).
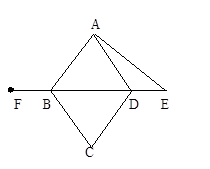
(1)连接 ;
(2)猜想: = ;
(3)证明:
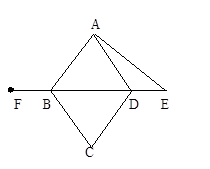
(1)连接 ;
(2)猜想: = ;
(3)证明:
(1)连结AF
(2)AF=AE
(3)证明:
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE(SAS)
∴AF=AE
(2)AF=AE
(3)证明:
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE(SAS)
∴AF=AE
试题分析:根据观察图形,应该是连接AF或者CF
(1)连结AF(或连结CF)
(2)猜想AF=AE(连结CF的,则猜想CF=AE)
(3)证明:(以AF=AE为例,其他证法参照得分)
∵四边形ABCD是菱形
∴AB=AD
∴∠ADB=∠ABD
∵∠ABD+∠ABF=180°
∠ADB+∠ADE=180°
∴∠ABF=∠ADE
∵BF = DE
∴△ABF≌△ADE(SAS)
∴AF=AE
点评:基本的几何综合题,考查简单的线段相等,可以通过全等三角形来证明。
三角形全等的判定定理:SSS、SAS、ASA。

练习册系列答案
相关题目
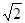 cm²
cm²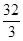
 cm²
cm² 中,
中,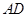 ∥
∥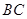 ,
,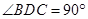 ,
, 为
为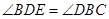 .
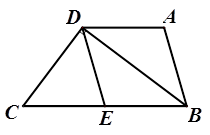
.
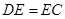 ;
; ,试判断四边形
,试判断四边形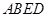 的形状,并说明理由.
的形状,并说明理由.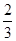 AO,ON=
AO,ON=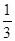 OD,设
OD,设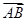 =
=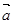 ,
,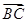 =
=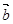 ,试用
,试用 和向量
和向量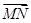 .
.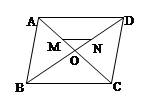
 是平行四边形的是( )
是平行四边形的是( )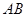 ∥
∥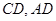 ∥
∥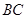
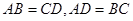
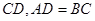
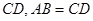
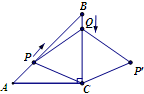
 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPCP′为菱形,则t的值为_________.
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPCP′为菱形,则t的值为_________.