题目内容
【题目】已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.
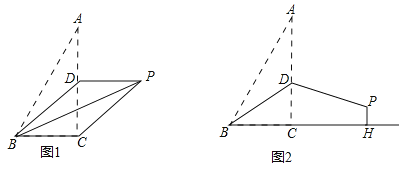
(1)如图1,若点D是AC中点,连接PC.
①写出BP,BD的长;
②求证:四边形BCPD是平行四边形.
(2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.
【答案】(1)①BD=![]() ,BP=
,BP=![]() ;②证明见解析;(2)
;②证明见解析;(2)![]() .
.
【解析】试题(1)①分别在Rt△ABC,Rt△BDC中,求出AB、BD即可解决问题;
②证明DP∥BC,DP=BC即可;
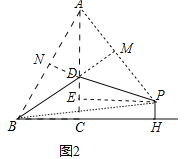
(2)如图2中,作DN⊥AB于N,PE⊥AC于E,延长BD交PA于M.设BD=AD=x,则CD=4﹣x.在Rt△BDC中,可得x2=(4﹣x)2+22,推出x的值,从而得出DN的长.由△BDN∽△BAM,可得![]() ,由此求出AM.由△ADM∽△APE,可得
,由此求出AM.由△ADM∽△APE,可得![]() ,由此求出AE的长,可得EC的长,由此即可解决问题.
,由此求出AE的长,可得EC的长,由此即可解决问题.
试题解析:解:(1)①在Rt△ABC中,∵BC=2,AC=4,∴AB=![]() =
=![]() .∵AD=CD=2,∴BD=
.∵AD=CD=2,∴BD=![]() =
=![]() .由翻折可知:BP=BA=
.由翻折可知:BP=BA=![]() .
.
②如图1中,∵△BCD是等腰直角三角形,∴∠BDC=45°,∴∠ADB=∠BDP=135°,∴∠PDC=135°﹣45°=90°,∴∠BCD=∠PDC=90°,∴DP∥BC,∵PD=AD=BC=2,∴四边形BCPD是平行四边形.

(2)如图2中,作DN⊥AB于N,PE⊥AC于E,延长BD交PA于M.设BD=AD=x,则CD=4﹣x.在Rt△BDC中,∵BD2=CD2+BC2,∴x2=(4﹣x)2+22,∴x=![]() .∵DB=DA,DN⊥AB,∴BN=AN=
.∵DB=DA,DN⊥AB,∴BN=AN=![]() .在Rt△BDN中,DN=
.在Rt△BDN中,DN=![]() =
=![]() .由△BDN∽△BAM,可得
.由△BDN∽△BAM,可得![]() ,∴
,∴![]() ,∴AM=2,∴AP=2AM=4.由△ADM∽△APE,可得
,∴AM=2,∴AP=2AM=4.由△ADM∽△APE,可得![]() ,∴
,∴![]() ,∴AE=
,∴AE=![]() ,∴EC=AC﹣AE=4﹣
,∴EC=AC﹣AE=4﹣![]() =
=![]() .易证四边形PECH是矩形,∴PH=EC=
.易证四边形PECH是矩形,∴PH=EC=![]() .
.

【题目】经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:
商品 | 红枣 | 小米 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 40 | 38 |
售价(元/袋) | 60 | 54 |
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣味x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.