题目内容
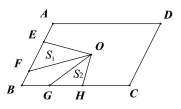
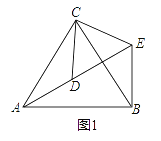
【题目】如图1,已知点A(0,a),点B(b,0),其中a,b满足![]() =0,点C(m,n)在第一象限,已知
=0,点C(m,n)在第一象限,已知![]() 是2的立方根.
是2的立方根.

(1)直接写出A,B,C三点的坐标;
(2)求出△ABC的面积;
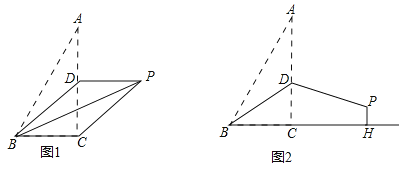
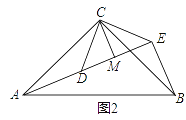
(3)如图2,延长BC交y轴于D点,求点D的坐标.
【答案】(1)点A的坐标为(0,2),点B的坐标为(8,0),点C的坐标为(4,4);(2)△ABC的面积=12;(3)点D的坐标为(0,8).
【解析】
(1)根据非负数的性质列出方程组分别求出a、b,根据立方根的概念求出m、n,得到A,B,C三点的坐标;
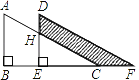
(2)作CE⊥y轴于点E,根据梯形的面积公式、三角形的面积公式计算;
(3)利用待定系数法求出直线BC的解析式,根据坐标轴上点的坐标特征计算,得到答案.
(1)由题意得,![]() ,
,
解得,![]() ,
,
∵![]() 是2的立方根,
是2的立方根,
∴n-1=3,m-2=2,
解得,m=4,n=4,
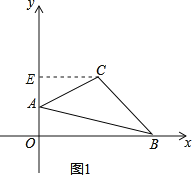
∴点A的坐标为(0,2),点B的坐标为(8,0),点C的坐标为(4,4);
(2)作CE⊥y轴于点E,
则△ABC的面积=梯形EOBC的面积-△AEC的面积-△AOB的面积
=![]() ×(4+8)×4-
×(4+8)×4-![]() ×4×2-
×4×2-![]() ×2×8
×2×8
=12;
(3)设直线BC的解析式为:y=kx+b,
则![]() ,
,
解得,![]() ,
,
∴直线BC的解析式为:y=-x+8,
当y=0时,-x+8=0,
解得,x=8,
∴点D的坐标为(0,8).

【题目】某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为__________________元(用含a的代数式表示);
当x≥16时,支付费用为_________________元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
物品重量(千克) | 支付费用(元) |
18 | 39 |
25 | 53 |
试根据以上提供的信息确定a,b的值.
(3)根据这个规定,若丙要托运一件超过16千克的物品,但支付的费用不想超过70元,那么丙托运的物品最多是多少千克.