Question

【题目】如图，已知∠ABC=90°，D是直线AB上的点，AD=BC．

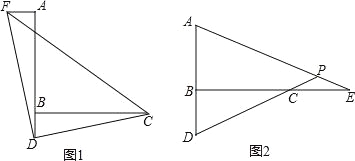
（1）如图1，过点A作AF⊥AB，并截取AF=BD，连接DC、DF、CF，判断△CDF的形状并证明；

（2）如图2，E是直线BC上一点，且CE=BD，直线AE、CD相交于点P，∠APD的度数是一个固定的值吗？若是，请求出它的度数；若不是，请说明理由．

Answer 1

【答案】（1）见解析；

（2）∠APD=∠FCD=45°．

【解析】

试题分析：（1）利用SAS证明△AFD和△BDC全等，再利用全等三角形的性质得出FD=DC，即可判断三角形的形状；

（2）作AF⊥AB于A，使AF=BD，连结DF，CF，利用SAS证明△AFD和△BDC全等，再利用全等三角形的性质得出FD=DC，∠FDC=90°，即可得出∠FCD=∠APD=45°．

试题解析：（1）△CDF是等腰直角三角形，理由如下：

∵AF⊥AD，∠ABC=90°，∴∠FAD=∠DBC，

在△FAD与△DBC中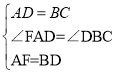，，∴△FAD≌△DBC（SAS），

∴FD=DC，∴△CDF是等腰三角形，∵△FAD≌△DBC，∴∠FDA=∠DCB，

∵∠BDC+∠DCB=90°，∴∠BDC+∠FDA=90°，

∴△CDF是等腰直角三角形；

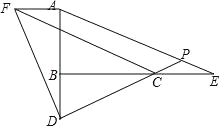
（2）作AF⊥AB于A，使AF=BD，连结DF，CF，如图，∵AF⊥AD，∠ABC=90°，

∴∠FAD=∠DBC，在△FAD与△DBC中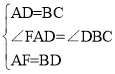，，∴△FAD≌△DBC（SAS），

∴FD=DC，∴△CDF是等腰三角形，∵△FAD≌△DBC，∴∠FDA=∠DCB，

∵∠BDC+∠DCB=90°，∴∠BDC+∠FDA=90°，∴△CDF是等腰直角三角形，

∴∠FCD=45°，∵AF∥CE，且AF=CE，∴四边形AFCE是平行四边形，

∴AE∥CF，∴∠APD=∠FCD=45°．