题目内容
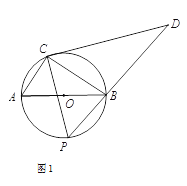
【题目】如图1,⊙O的直径AB为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧![]() 向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
(1)求证:△ABC∽△PDC
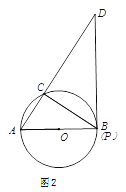
(2)如图2,当点P到达B点时,求CD的长;
(3)设CD的长为![]() .在点P的运动过程中,
.在点P的运动过程中,![]() 的取值范围为 (请直接写出答案).
的取值范围为 (请直接写出答案).
【答案】(1)证明见解析;(2)6;(3)![]()
【解析】试题分析:(1)利用圆周角定理得出∠ACB=90°,进而得出∠ACB=∠PCD和∠A=∠P,从而得解;
(2)先求出BC,根据三角形相似可求CD的长;
(3)如图中,由题意可知CD=PCtan60°,所以只要求出PC的最小值和最大值即可解决问题.
试题解析:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠PCD,
又∵∠A=∠P,
∴△ABC∽△PDC
(2)∵∠ABC=30°,AB=4,
∴BC=![]() ,
,
∵△ABC∽△PDC,
∴∠D=∠ABC=30°,
∴CD=6
(3)如图,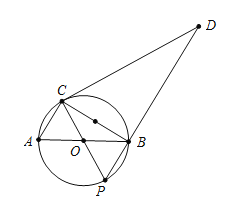
∵AB是直径,∠ABC=30°,AB=4
∴∠ACB=90°,∠A=∠P=60°,AC=2,
∵CD⊥PC,
∴∠PCD=90°,CD=PCtan60°,
∵PC的最小值=AC=2,PC的最大值为直径=4,
∴CD的最小值为2![]() ,最大值为4
,最大值为4![]() ,
,
∴2![]() ≤CD≤4
≤CD≤4![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,如表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
17吨及以下 | a | 0.80 |
超过17吨不超过30吨的部分 | b | 0.80 |
超过30吨的部分 | 6.0 | 0.80 |
(说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
(1)已知小王家2016年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元,求a、b的值.
(2)如果6月份小王家计划水费不超过140元,那么他家本月用水量最多为多少吨?