Question

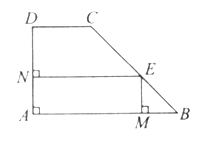
如下图，直角梯形ABCD中，AD∥BC，AD=24cm，BC=26cm，∠B=90°，动点P从A开始沿AD边向D以1cm/s的速度运动，动点Q从点C开始沿CB以3cm/s的速度向点B运动、P、Q同时出发，当其中一点到达顶点时，另一点也随之停止运动，设运动时间为ts，问t为何值时，
（1）四边形PQCD是平行四边形．
（2）当t为何值时，四边形PQCD为等腰梯形．

Answer 1

解：（1）∵PD∥CQ，∴当PD=CQ时，四边形PQCD是平行四边形．
而PD=24-t，CQ=3t，
∴24一t=3t，解得t=6．
当t=6时，四边形PQCD是平行四边形．

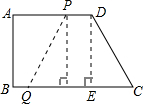
（2）如图，过点D作DE⊥BC，则CE=BC-AD=2cm．
当CQ-PD=4时，四边形PQCD是等腰梯形．
即3t-（24-t）=4
∴t=7．
分析：（1）首先列出各点在各段上的函数关系式，PD=24-t，CQ=3t，按照平行四边形性质可知使PD=CQ，即可得出结论．
（2）根据等腰梯形的可知，过点D、P做DE⊥BC于E，PF⊥CD于F，即有FQ=CE，又CE=BC-AD=4．所以，3t-（24-t）=4，可解
点评：要求学生掌握对各种图形的认识，同时学会数形结合的数学解题思想．