题目内容
如下图所示，在直角梯形ABCD中，AB∥CD，∠A＝90°，点E为AD的中点，P在腰BC上且不与B，C重合，连接PD，PE，AB＝18，CD＝6，AD＝16，设PC＝x，S△PDE＝y．
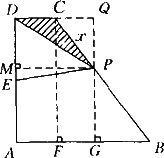
(1)求y与x之间的函数关系式；
(2)x为何值时，tan∠DPE＝
？
(3)是否存在x，使S△DPC＝
S梯形ABCD？
答案：
解析：
解析：
|
分析：本题属于存在探索题，即当点P在腰BC上时，是否存在△PDC，使S△DPC＝ |
S梯形ABCD．解题方法是假设存在满足条件的△DPC，经过推理、计算，看是否能得出矛盾．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
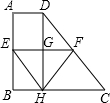如图所示，在直角梯形ABCD中，AB⊥BC，AD=1，BC=3，CD=4，EF为梯形的中位线，DH为梯形的高且交EF于点G，下列结论：①G为EF的中点；②△EHF为等边三角形；③四边形EHCF为菱形；④S△BEH=S△CFH，其中正确的结论有（ ）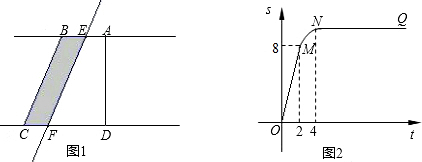
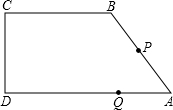
达自己的终点时，另一个点也停止运动，设这两个点从出发运动了t秒．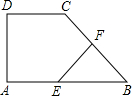
（2013•山西模拟）如图所示，在直角梯形ABCD中，AB∥CD，点E为AB的中点，点F为BC的中点，AB=4，EF=2，∠B=60°，则AD的长为