题目内容
【题目】如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，下列结论：
①∠AED=90° ②∠ADE=∠CDE ③DE=BE ④AD=AB+CD，
四个结论中成立的是（ ）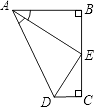
A.①②④
B.①②③
C.②③④
D.①③
【答案】A
【解析】解：过E作EF⊥AD于F，如图，
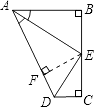
∵AB⊥BC，AE平分∠BAD，
∴Rt△AEF≌Rt△AEB
∴BE=EF，AB=AF，∠AEF=∠AEB；
而点E是BC的中点，
∴EC=EF=BE，所以③错误；
∴Rt△EFD≌Rt△ECD，
∴DC=DF，∠FDE=∠CDE，所以②正确；
∴AD=AF+FD=AB+DC，所以④正确；
∴∠AED=∠AEF+∠FED= 
∠BEC=90°，所以①正确．
所以答案是：A．
【考点精析】掌握角平分线的性质定理是解答本题的根本，需要知道定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上．
练习册系列答案
相关题目
