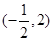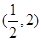题目内容
函数y= 和y=
和y= 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y= 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y= 的图象于点A. PD⊥y轴于点D,交y=
的图象于点A. PD⊥y轴于点D,交y= 的图象于点B。.下面结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B。.下面结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA= AP. 其中正确结论是
AP. 其中正确结论是

A.①②③ B.①②④ C.①③④ D.②③④
 和y=
和y= 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y= 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y= 的图象于点A. PD⊥y轴于点D,交y=
的图象于点A. PD⊥y轴于点D,交y= 的图象于点B。.下面结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B。.下面结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA= AP. 其中正确结论是
AP. 其中正确结论是
A.①②③ B.①②④ C.①③④ D.②③④
C
试题分析:解:∵A、B是反比函数y=
 上的点,
上的点,∴S△OBD=S△OAC=
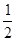 ,故①正确;
,故①正确;∵当P的横纵坐标相等时PA=PB,故②错误;
∵P是反比例函数y=
 上的点,
上的点,∴S矩形PDOC=4,
∴S四边形PAOB=S矩形PDOC-S△ODB--S△OAC=4-
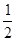 -
-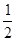 =3,故③正确;
=3,故③正确;连接OP,
∵
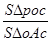 =
=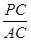 =
=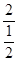 =4
=4∴AC=
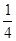 PC,PA=
PC,PA=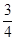 PC,
PC,∴
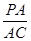 =3,
=3,同理可得
 =3
=3∴
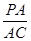 =
= ,故④正确.
,故④正确.故答案为:①③④
点评:此题比较综合,把反比例函数和三角形,四边形的面积及相似比结合起来考察,要求学生对知识的熟练程度比较高。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
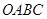 的顶点
的顶点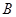 在
在 轴上,顶点
轴上,顶点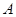 的坐标为
的坐标为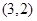 .若反比例函数
.若反比例函数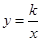 的图象经过点
的图象经过点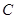 ,则
,则 的值为
的值为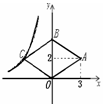
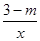 的图象上有两点A(x1,y1)和B(x2,y2),且当x1<0<x2时,有y1<y2,则m的取值范围是 .
的图象上有两点A(x1,y1)和B(x2,y2),且当x1<0<x2时,有y1<y2,则m的取值范围是 .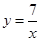 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为 .
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为 .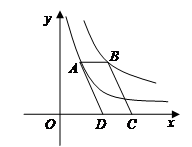
 轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线
轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.若
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.若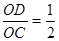 ,
,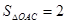 ,则
,则 的值为 .
的值为 .
 (x<0)和
(x<0)和 (x>0)的图象上,分别有A、B两点,若AB∥x轴且OA⊥OB,则A点坐标为 .
(x>0)的图象上,分别有A、B两点,若AB∥x轴且OA⊥OB,则A点坐标为 .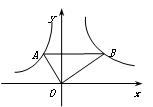
 (x>o)的一个分支上,点B在x轴上,CD⊥OB于D,若△AOC的面积为3,则k的值为
(x>o)的一个分支上,点B在x轴上,CD⊥OB于D,若△AOC的面积为3,则k的值为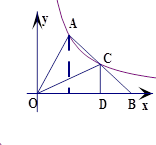

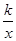 的图象经过点(-1,2),则这个函数的图象一定过点( )
的图象经过点(-1,2),则这个函数的图象一定过点( )