题目内容
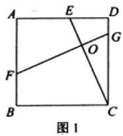
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E. 
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积S.
【答案】
(1)解:∵∠D=60°,
∴∠B=60°(圆周角定理),
又∵AB=6,
∴BC=3,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OE⊥AC,
∴OE∥BC,
又∵点O是AB中点,
∴OE是△ABC的中位线,
∴OE= ![]() BC=
BC= ![]()
(2)解:连接OC,

则易得△COE≌△AFE,
故阴影部分的面积=扇形FOC的面积,
S扇形FOC= ![]() =
= ![]() π.
π.
即可得阴影部分的面积为 ![]() π
π
【解析】(1)根据∠D=60°,可得出∠B=60°,继而求出BC,判断出OE是△ABC的中位线,就可得出OE的长;(2)连接OC,将阴影部分的面积转化为扇形FOC的面积.
【考点精析】认真审题,首先需要了解含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目