Question

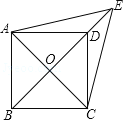
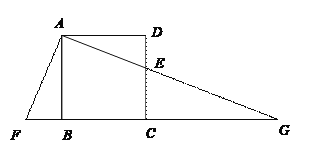
【题目】如图，E是正方形ABCD的边DC上的一点，过A作AF⊥AE，交CB延长线于点F．AE的延长线交BC的延长线于点G．

（1）求证：AE=AF；

（2）若AF=7，DE=2，求EG的长．

Answer 1

【答案】（1）见解析；（2）．

【解析】分析：（1）首先利用余角的性质证明∠FAB=∠DAE，然后利用ASA即可证明△ABF≌△ADE，根据全等三角形的对应边相等即可证得；

（2）在直角△ABF中利用勾股定理求得AB的长，则EC的长度即可求得，易证△ADE∽△GCE，根据相似三角形的对应边的比相等即可求解．

详解：（1）证明：正方形ABCD中，∠BAD=90°，AD=AB，

∵AF⊥AE，∴∠FAB+∠BAE=90°．

∵∠DAE+∠BAE=90°,

∴∠FAB=∠DAE．

∵∠FBA=∠D=90°，

∴△ABF≌△ADE．

∴AE=AF．

（2）解：在Rt△ABF中，∠FBA=90°,AF=7,BF=DE=2．

∴AB=,

∴EC=DC-DE=．

∵∠D=∠ECG=90°，∠DEA=∠CEG，

∴△ADE∽△GCE．

∴

∴EG=．