ћвƒњƒЏ»Ё
°Њћвƒњ°њ£®2014Ї”ƒѕ21ћв£©ƒ≥…ћµкѕъ џ10ћ®A–ЌЇЌ20ћ®B–Ќµзƒ‘µƒјы»уќ™4000‘™£ђѕъ џ20ћ®A–ЌЇЌ10ћ®B–Ќµзƒ‘µƒјы»уќ™3500‘™£Ѓ
£®1£©«у√њћ®A–Ќµзƒ‘ЇЌB–Ќµзƒ‘µƒѕъ џјы»у£ї
£®2£©Є√…ћµкЉ∆їЃ“їіќєЇљшЅљ÷÷–ЌЇ≈µƒµзƒ‘є≤100ћ®£ђ∆д÷–B–Ќµзƒ‘µƒљшїхЅњ≤ї≥ђєэA–Ќµзƒ‘µƒ2±ґ£Ѓ…иєЇљшA–Ќµзƒ‘xћ®£ђ’в100ћ®µзƒ‘µƒѕъ џ„№јы»уќ™y‘™£Ѓ
Ґў«уyєЎ”ЏxµƒЇѓ эєЎѕµ љ£ї
ҐЏЄ√…ћµкєЇљшA–Ќ°ҐB–Ќµзƒ‘Єчґа…ўћ®£ђ≤≈ƒ№ єѕъ џ„№јы»у„оіу£њ
£®3£© µЉ љшїх ±£ђ≥ІЉ“ґ‘A–Ќµзƒ‘≥ц≥ІЉџѕ¬љµ![]() ‘™£ђ«“ѕёґ®…ћµк„оґаєЇљшA–Ќµзƒ‘70ћ®£Ѓ»ф…ћµк±£≥÷Ѕљ÷÷µзƒ‘µƒ џЉџ≤ї±д£ђ«лƒгЄщЊЁ“‘…ѕ–≈ѕҐЉ∞£®2£©÷–ћхЉю£ђ…иЉ∆≥ц є’в100ћ®µзƒ‘ѕъ џ„№јы»у„оіуµƒљшїхЈљ∞Є£Ѓ
‘™£ђ«“ѕёґ®…ћµк„оґаєЇљшA–Ќµзƒ‘70ћ®£Ѓ»ф…ћµк±£≥÷Ѕљ÷÷µзƒ‘µƒ џЉџ≤ї±д£ђ«лƒгЄщЊЁ“‘…ѕ–≈ѕҐЉ∞£®2£©÷–ћхЉю£ђ…иЉ∆≥ц є’в100ћ®µзƒ‘ѕъ џ„№јы»у„оіуµƒљшїхЈљ∞Є£Ѓ
°Њір∞Є°њ£®1£©√њћ®![]() –Ќµзƒ‘µƒѕъ џјы»уќ™100‘™£ђ√њћ®
–Ќµзƒ‘µƒѕъ џјы»уќ™100‘™£ђ√њћ®![]() –Ќµзƒ‘µƒѕъ џјы»уќ™150‘™£ї£®2£©Ґў
–Ќµзƒ‘µƒѕъ џјы»уќ™150‘™£ї£®2£©Ґў![]() £їҐЏ…ћµкєЇљш
£їҐЏ…ћµкєЇљш![]() –Ќµзƒ‘34ћ®£ђ
–Ќµзƒ‘34ћ®£ђ![]() –Ќµзƒ‘66ћ®£ђ≤≈ƒ№ єѕъ џ„№јы»у„оіу£ї£®3£©µ±
–Ќµзƒ‘66ћ®£ђ≤≈ƒ№ єѕъ џ„№јы»у„оіу£ї£®3£©µ±![]() ±£ђ…ћµкєЇљш34ћ®
±£ђ…ћµкєЇљш34ћ®![]() –Ќµзƒ‘ЇЌ66ћ®
–Ќµзƒ‘ЇЌ66ћ®![]() –Ќµзƒ‘≤≈ƒ№їсµ√„оіујы»у£їµ±
–Ќµзƒ‘≤≈ƒ№їсµ√„оіујы»у£їµ±![]() ±£ђ…ћµкєЇљш
±£ђ…ћµкєЇљш![]() –Ќµзƒ‘ эЅњ¬ъ„г
–Ќµзƒ‘ эЅњ¬ъ„г![]() µƒ’ы э ±£ђЊщїсµ√„оіујы»у£їµ±
µƒ’ы э ±£ђЊщїсµ√„оіујы»у£їµ±![]() ±£ђ…ћµкєЇљш70ћ®
±£ђ…ћµкєЇљш70ћ®![]() –Ќµзƒ‘ЇЌ30ћ®
–Ќµзƒ‘ЇЌ30ћ®![]() –Ќµзƒ‘≤≈ƒ№їсµ√„оіујы»у£Ѓ
–Ќµзƒ‘≤≈ƒ№їсµ√„оіујы»у£Ѓ
°Њљвќц°њ
£®1£©…и√њћ®![]() –Ќµзƒ‘µƒѕъ џјы»уќ™
–Ќµзƒ‘µƒѕъ џјы»уќ™![]() ‘™£ђ√њћ®
‘™£ђ√њћ®![]() –Ќµзƒ‘µƒѕъ џјы»уќ™
–Ќµзƒ‘µƒѕъ џјы»уќ™![]() ‘™£ђ‘т”–
‘™£ђ‘т”–
![]() £ђ
£ђ![]() љвµ√
љвµ√
![]()
ір£Ї√њћ®![]() –Ќµзƒ‘µƒѕъ џјы»уќ™100‘™£ђ√њћ®
–Ќµзƒ‘µƒѕъ џјы»уќ™100‘™£ђ√њћ®![]() –Ќµзƒ‘µƒѕъ џјы»уќ™150‘™£ї
–Ќµзƒ‘µƒѕъ џјы»уќ™150‘™£ї
£®2£©ҐўЄщЊЁћв“вµ√![]() £ђЉі
£ђЉі
![]() £ї
£ї
ҐЏЄщЊЁћв“вµ√£Ї![]() £ђљвµ√
£ђљвµ√![]() £Ѓ
£Ѓ
![]() ÷–£ђ
÷–£ђ![]() £ђ
£ђ
![]() Ћж
Ћж![]() µƒ‘ціуґшЉх–°£Ѓ
µƒ‘ціуґшЉх–°£Ѓ
![]() ќ™’э’ы э£ђ
ќ™’э’ы э£ђ
°аµ±![]() ±£ђ
±£ђ![]() »°µ√„оіу÷µ£ђіЋ ±
»°µ√„оіу÷µ£ђіЋ ±![]() £Ѓ
£Ѓ
ір£Ї…ћµкєЇљш![]() –Ќµзƒ‘34ћ®£ђ
–Ќµзƒ‘34ћ®£ђ![]() –Ќµзƒ‘66ћ®£ђ≤≈ƒ№ єѕъ џ„№јы»у„оіу£ї
–Ќµзƒ‘66ћ®£ђ≤≈ƒ№ єѕъ џ„№јы»у„оіу£ї
£®3£©ЄщЊЁћв“вµ√![]() £ђ
£ђ
Љі![]() £ђ∆д÷–
£ђ∆д÷–![]() £Ѓ
£Ѓ
Ґўµ±![]() ±£ђ
±£ђ![]() £ђ
£ђ
![]() Ћж
Ћж![]() µƒ‘ціуґшЉх–°£ђ
µƒ‘ціуґшЉх–°£ђ
°аµ±![]() ±£ђ
±£ђ![]() »°µ√„оіу÷µ£ђ
»°µ√„оіу÷µ£ђ
Љі…ћµкєЇљш34ћ®![]() –Ќµзƒ‘ЇЌ66ћ®
–Ќµзƒ‘ЇЌ66ћ®![]() –Ќµзƒ‘≤≈ƒ№їсµ√„оіујы»у£ї
–Ќµзƒ‘≤≈ƒ№їсµ√„оіујы»у£ї
ҐЏµ±![]() ±£ђ
±£ђ![]() £ђ
£ђ![]() £ђ
£ђ
Љі…ћµкєЇљш![]() –Ќµзƒ‘ эЅњ¬ъ„г
–Ќµзƒ‘ эЅњ¬ъ„г![]() µƒ’ы э ±£ђЊщїсµ√„оіујы»у£ї
µƒ’ы э ±£ђЊщїсµ√„оіујы»у£ї
Ґџµ±![]() ±£ђ
±£ђ![]() £ђ
£ђ
![]() Ћж
Ћж![]() µƒ‘ціуґш‘ціу£Ѓ
µƒ‘ціуґш‘ціу£Ѓ
°аµ±![]() ±£ђ
±£ђ![]() »°µ√„оіу÷µ£Ѓ
»°µ√„оіу÷µ£Ѓ
Љі…ћµкєЇљш70ћ®![]() –Ќµзƒ‘ЇЌ30ћ®
–Ќµзƒ‘ЇЌ30ћ®![]() –Ќµзƒ‘≤≈ƒ№їсµ√„оіујы»у£Ѓ
–Ќµзƒ‘≤≈ƒ№їсµ√„оіујы»у£Ѓ

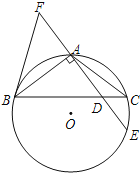
°Њћвƒњ°њ»зЌЉ1÷ЅЌЉ3 «љЂ’эЈљћељЎ»•“ї≤њЈ÷Їуµ√µљµƒЉЄЇќће£Ѓ

(1)ЄщЊЁ“™«ућо–і±нЄс£Ї
√ж э/f | ґ•µг э/v | јв э/e | |
ЌЉ1 | _____ | _____ | ____ |
ЌЉ2 | _____ | _____ | _____ |
ЌЉ3 | ___ | _____ | ____ |
(2)≤¬ѕлf£ђv£ђe»эЄц эЅњЉдµƒєЎѕµ£Ѓ
(3)ЄщЊЁ≤¬ѕлЉ∆Ћг£ђ»ф“їЄцЉЄЇќћеµƒґ•µг”–2 019Єц£ђјв”–4 035ћх£ђ ‘«у≥цЋьµƒ√ж э£Ѓ