题目内容
 如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=________cm,点O到AB的距离为________cm.
如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=________cm,点O到AB的距离为________cm.
5 3
分析:连接OC,OB,交于AB点M,根据圆周角定理推出△OBC为等边三角形,即可得出半径OB的长度;然后根据垂径定理推出BM的长度,根据勾股定理即可得出OM的长度,即O点到AB的距离.
解答: 解:连接OC,OB,交AB于点M,
解:连接OC,OB,交AB于点M,
∵∠A=30°,BC=5cm,
∴∠COB=60°,
∵OB=OC,BC=5,
∴OB=OC=BC=5
∵AB=8cm,
∴AM=BM=4,
∵OM⊥AB,
∴OM=3.
故答案为5,3.
点评:本题主要考查圆周角定理、勾股定理、垂径定理,关键在于正确地作出辅助线,推出圆的半径.
分析:连接OC,OB,交于AB点M,根据圆周角定理推出△OBC为等边三角形,即可得出半径OB的长度;然后根据垂径定理推出BM的长度,根据勾股定理即可得出OM的长度,即O点到AB的距离.
解答:
 解:连接OC,OB,交AB于点M,
解:连接OC,OB,交AB于点M,∵∠A=30°,BC=5cm,
∴∠COB=60°,
∵OB=OC,BC=5,
∴OB=OC=BC=5
∵AB=8cm,
∴AM=BM=4,
∵OM⊥AB,
∴OM=3.
故答案为5,3.
点评:本题主要考查圆周角定理、勾股定理、垂径定理,关键在于正确地作出辅助线,推出圆的半径.

练习册系列答案
相关题目
 24、如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.
24、如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.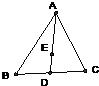 14、如图,E为△ABC的重心,ED=3,则AD=
14、如图,E为△ABC的重心,ED=3,则AD= (2012•井研县模拟)如图,D为△ABC的AB边上的一点,∠ABC=∠ACD,AD=2cm,AB=3cm,则AC=( )
(2012•井研县模拟)如图,D为△ABC的AB边上的一点,∠ABC=∠ACD,AD=2cm,AB=3cm,则AC=( )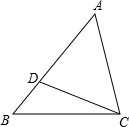 如图,D为△ABC的边AB上一点,且∠ABC=∠ACD,AD=3cm,AB=4cm,则AC的长为( )
如图,D为△ABC的边AB上一点,且∠ABC=∠ACD,AD=3cm,AB=4cm,则AC的长为( )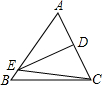 如图,DE为△ABC中AC边的中垂线,BC=8,AB=10,则△EBC的周长是( )
如图,DE为△ABC中AC边的中垂线,BC=8,AB=10,则△EBC的周长是( )