题目内容
（2012•长春一模）如图，河旁有一座小山，从山顶A处测得河对岸点C的俯角为31°，测得岸边点D的俯角为45°．又知河宽CD为50米，求小山的高度．【参考数据：sin31°=0.52，cos31°=0.86，tan31°=0.60】
分析：用含AB的式子表示出BC，BD．再根据BC-BD=CD=50得方程即可求出山高AB．
解答：解：设山高AB为x．
在Rt△ACB中有：CB=
=
x，
在Rt△ADB中有：BD=
=x．
而CD=CB-BD=（
-1）x=50，
解得x=75．
故小山的高度为75米．
在Rt△ACB中有：CB=
| x |
| tan31° |
| 5 |
| 3 |
在Rt△ADB中有：BD=
| x |
| tan45° |
而CD=CB-BD=（
| 5 |
| 3 |
解得x=75．
故小山的高度为75米．
点评：本题考查运用三角函数的定义解直角三角形．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
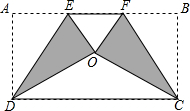（2012•长春一模）将矩形纸片ABCD按如图方式折叠，DE、CF为折痕，折叠后点A和点B都落在点O处．若△EOF是等边三角形，则
（2012•长春一模）如图，抛物线y=ax2-x-
-B于点P，以PQ为一边向右作正方形PQRS，设运动时间为t（秒），正方形PQRS与梯形OABC重叠面积为S（平方单位）