题目内容
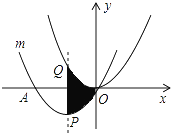
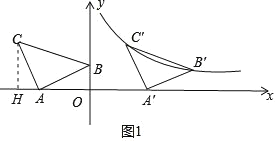
【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(3,0),B(0,1)

(1)将△ABC沿x轴的正方向平移t个单位,B、C两点的对应点B′、C′正好落在反比例函数y=![]() 的图象上.请直接写出C点的坐标和t,k的值;
的图象上.请直接写出C点的坐标和t,k的值;
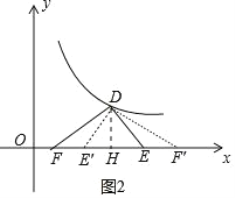
(2)有一个Rt△DEF,∠D=90°,∠E=60°,DE=2,将它放在直角坐标系中,使斜边EF在x轴上,直角顶点D在(1)中的反比例函数图象上,求点F的坐标;
(3)在(1)的条件下,问是否存在x轴上的点M和反比例函数y=![]() 图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
【答案】(1)C(4,3),t=6,k=6;(2)满足条件的点F的坐标为(![]() 3,0)或(
3,0)或(![]() +3,0);(3)存在,点N(3,2),M(7,0)时,四边形MNC′B′是平行四边形,当N′(3,2),M(7,0)时,四边形M′N′B′C′是平行四边形
+3,0);(3)存在,点N(3,2),M(7,0)时,四边形MNC′B′是平行四边形,当N′(3,2),M(7,0)时,四边形M′N′B′C′是平行四边形
【解析】
(1)过C点作CH⊥x轴,构造△CAH≌△ABO,从而确定C点坐标,根据坐标平移规律沿x轴的正方向平移t个单位可得B′(t、1)、C′(-4+t,3),根据反比例函数性质可求出t,然后可求出k;
(2)分情况画出斜边在x轴,直角顶点D在反比例图象上,先求出直角三角形斜边的高,即D点的y值,即可解决问题.
(3)分两种情形:①线段B′C′为平行四边形的边时.②线段B′C′是对角线时,分别求解即可.
(1)如图1中,过C点作CH⊥x轴,垂足为H,
∵∠BAC=∠AOB=∠CHA=90°,
∴∠CAH+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠CAH=∠ABO,
∵AC=AB,
∴△CHA≌△AOB(AAS),
∴AH=OB=1,OA=CH=3,
∴C(4,3),B(0,1),
由题意![]() (4+t,3),
(4+t,3),![]() (t,1),
(t,1),
∵![]() ,
,![]() 都在y=
都在y=![]() 上,
上,
∴(4+t)×3=t×1,
∴t=6,
∴![]() (6,1),
(6,1),
∴k=6.
(2)如图2中,作DH⊥x轴于H.
在Rt△DEF中,∵∠EDF=90°,∠DEF=60°,DE=2,
∴EF=4,DF=![]() ,
,
∵![]() DFDE=
DFDE=![]() EFDH,
EFDH,
∴DH=![]() ,
,
∴FH=3,EH=1,D(![]() ,
,![]() ),
),
∴OF=![]() 3,
3,
∴F(![]() 3,0),
3,0),
当点![]() 在点
在点![]() 右侧时,
右侧时,![]() (
(![]() +3,0).
+3,0).
综上所述,满足条件的点F的坐标为(![]() 3,0)或(
3,0)或(![]() +3,0).
+3,0).
(3)由(1)可知:![]() (6,1),
(6,1),![]() (2,3).
(2,3).

当点N(3,2),M(7,0)时,四边形![]() 是平行四边形,
是平行四边形,
当![]() (3,2),M(7,0)时,四边形
(3,2),M(7,0)时,四边形![]() 是平行四边形.
是平行四边形.