题目内容
【题目】如图,在平面直角坐标系中,直线l: ![]() 与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.

【答案】(1)A1(![]() ,3),在直线上;(2)
,3),在直线上;(2)![]() ;(3)P1(
;(3)P1(![]() ,3),P2(
,3),P2(![]() ,﹣3),P3(﹣
,﹣3),P3(﹣![]() ,3).
,3).
【解析】试题分析:
(1) 根据题意画出示意图,过点A1作x轴的垂线AD,在Rt△A1DB1中利用等边三角形的性质和勾股定理可以求得线段A1D和B1D的长,进而写出点A1的坐标. 将点A1的横坐标代入直线l的解析式,求得相应的纵坐标,通过对比求得的纵坐标和点A1的纵坐标可以判断点A1与直线l的位置关系.
(2) 根据等边三角形的边长容易得到点C1的坐标. 利用点A1和点C1的坐标,结合一次函数的一般形式,可以获得关于待定系数的方程,求解这些方程进而可以写出边A1C1所在直线的解析式.
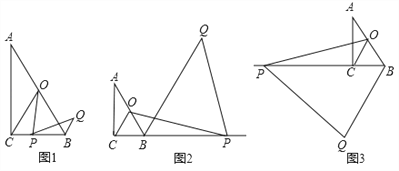
(3) 由于利用△A1C1M的三个内角均可以构造出符合题意的平行四边形,所以本小题应对这三种情况分别进行讨论. 根据题意画出各种情况的示意图. 当以∠A1C1M为平行四边形的一个内角构造平行四边形时,可以过点A1作y轴的垂线AE,利用Rt△A1B1E中的几何关系求得线段A1E和B1E的长. 利用点M的坐标和等边三角形的边长可以得到线段C1M的长,进而获得线段A1P的长,从而可以写出点P的坐标. 当以∠A1MC1为平行四边形的一个内角构造平行四边形时,利用Rt△A1B1F中的几何关系和线段C1M的长,可以求得线段A1F和B1F的长,进而写出点P的坐标. 当以∠C1A1M为平行四边形的一个内角构造平行四边形时,可以过点P作x轴的垂线PG,利用平行四边形的性质获得线段PM的长,利用Rt△PGM中的几何关系和线段B1M的长,可以求得线段PG和OG的长,进而写出点P的坐标.
试题解析:
(1) 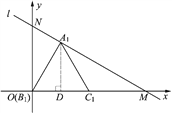
如图,过点A1作A1D⊥OM,垂足为D.
∵△A1B1C1是等边三角形,A1D⊥OM,
∴∠B1A1D=30°,
∴在Rt△A1DB1中, ![]() ,
,
∵A1D=3,
∴在Rt△A1DB1中, ![]() ,
,
∴![]() ,
, ![]() .
.
∴点A1的坐标为(![]() , 3).
, 3).
由直线l的解析式,得
当x=![]() 时,
时, ![]() ,
,
∴点A1在直线l上.
(2) ∵△A1B1C1是等边三角形, ![]() ,
,
∴![]() .
.
∴点C1的坐标为(![]() , 0).
, 0).
设直线A1C1的解析式为y=kx+b (k≠0).
将点A1 (![]() , 3),点C1 (
, 3),点C1 (![]() , 0)的坐标分别代入直线A1C1的解析式,得
, 0)的坐标分别代入直线A1C1的解析式,得
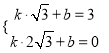 ,
,
解之,得
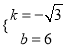 ,
,
∴直线A1C1的解析式为![]() .
.
(3) 点P的坐标为(![]() , 3),(
, 3),(![]() , 3)或(
, 3)或(![]() , -3). 求解过程如下.
, -3). 求解过程如下.
根据题意,分别对下面三种情况进行讨论.
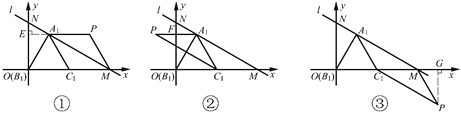
①若以∠A1C1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1MP.
如图①,过点A1作A1E⊥ON,垂足为E.
由直线l的解析式,得
当y=0时, ![]() ,
,
∴x=![]() .
.
∴点M的坐标为(![]() , 0).
, 0).
∴OM=![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵△A1B1C1是等边三角形,
∴∠A1B1C1=60°,
∴∠A1B1E=90°-∠A1B1C1=90°-60°=30°.
∴在Rt△A1EB1中, ![]() ,
, ![]() .
.
∵A1P∥C1M,A1E⊥ON,
∴点E,A1,P在同一条直线上,
∴![]() .
.
∴点P的坐标为(![]() , 3).
, 3).
②若以∠A1MC1为平行四边形的一个内角,则所求平行四边形为平行四边形PC1MA1.
∵A1P∥C1M,
∴A1F⊥ON,
∴在Rt△A1FB1中, ![]() ,
, ![]() .
.
∵![]() ,
,
∴![]() .
.
∴点P的坐标为(![]() , 3).
, 3).
③若以∠C1A1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1PM.
如图③,过点P作PG⊥OM,垂足为G.
∵△A1B1C1是等边三角形,
∴∠A1C1B1=60°,
∴∠A1C1M=180°-∠A1C1B1=180°-60°=120°,
∵A1C1∥PM,
∴∠PMC1=∠A1C1M=120°,
∴∠PMG=180°-∠PMC1=180°-120°=60°,
∴在Rt△PMG中,∠MPG=90°-∠PMG=90°-60°=30°.
∵![]() ,
,
∴在Rt△PGM中, ![]() ,
,
![]() .
.
∵OM=![]() ,
,
∴![]() .
.
∴点P的坐标为(![]() , -3).
, -3).
综上所述,点P的坐标为(![]() , 3),(
, 3),(![]() , 3)或(
, 3)或(![]() , -3).
, -3).

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案