题目内容
【题目】解下列方程(组):
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)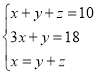 .
.
【答案】(1)x=-2;(2)x=-1;(3)![]() ;(4)
;(4)![]()
【解析】
(1)方程去括号,移项,合并同类项,系数化1,即可解出;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)①-②×3得出5y=-5,求出y,把y=-1代入①求出x即可;
(4)方程组利用加减消元法转化为二元方程逐步求出解即可.
解:(1)去括号得:4x+3=2x-2+1,
移项合并得:2x=-4,
解得:x=-2;
(2)去分母得:2(3x-2)=5(x+1)-10,
去括号得:6x-4=5x+5-10,
移项合并得:x=-1.
(3)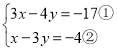
①-②×3得:5y=-5,
解得:y=-1,
把y=-1代入②得:x+3=-4,
解得:x=-7,
所以方程组的解为:![]()
(4)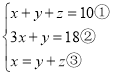
把③代入①得:y+z=5④,
把③代入②得:4y+3z=18⑤,
④×4-⑤得:z=2,
把z=2代入④得:y=3,
把y=3,z=2代入③得:x=5,
则方程组的解为![]() ,
,

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】问题探究:小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请你解决相关问题:
![]() 在函数
在函数![]() 中,自变量x可以是任意实数;
中,自变量x可以是任意实数;
![]() 如表y与x的几组对应值:
如表y与x的几组对应值:
X |
|
|
|
|
| 0 | 1 | 2 | 3 | 4 |
|
Y |
|
| 0 | 1 | 2 | 3 | 2 | 1 | a |
|
|
![]() ______;
______;
![]() 若
若![]() ,
,![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ______;
______;
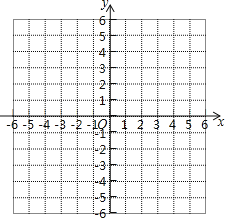
![]() 如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
![]() 该函数有______
该函数有______![]() 填“最大值”或“最小值”
填“最大值”或“最小值”![]() ;并写出这个值为______;
;并写出这个值为______;
![]() 求出函数图象与坐标轴在第二象限内所围成的图形的面积;
求出函数图象与坐标轴在第二象限内所围成的图形的面积;
![]() 观察函数
观察函数![]() 的图象,写出该图象的两条性质.
的图象,写出该图象的两条性质.