题目内容
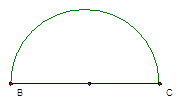
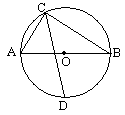
如图,在半圆O中,直径AE=10,四边形ABCD是平行四边形,且顶点A、B、C在半圆上,点D在直径AE上,连接CE,若AD=8,则CE长为 .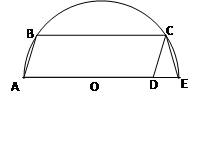


连接OC,过O点作BC垂线,设垂足为F,根据垂径定理、勾股定理可以得到OC=5,CF=4,OF=3,在等腰三角形CDE中,高=OF=3,底边长DE=10-8=2,根据勾股定理即可求出CE.

解:连接OC,过O点作OF⊥BC,垂足为F,交半圆与点H,
∵OC=5,BC=8,
∴根据垂径定理CF=4,点H为弧BC的中点,且为半圆AE的中点,
∴由勾股定理得OF=3,且弧AB=弧CE
∴AB=CE,
又∵ABCD为平行四边形,
∴AB=CD,
∴CE=CD,
∴△CDE为等腰三角形,
在等腰三角形CDE中,DE边上的高CM=OF=3,
∵DE=10-8=2,
∴由勾股定理得,CE2=OF2+( DE)2,
DE)2,
∴CE= ,
,
故答案为 .
.
本题考查了勾股定理和垂径定理以及平行四边形的性质,是基础知识要熟练掌握.

解:连接OC,过O点作OF⊥BC,垂足为F,交半圆与点H,
∵OC=5,BC=8,
∴根据垂径定理CF=4,点H为弧BC的中点,且为半圆AE的中点,
∴由勾股定理得OF=3,且弧AB=弧CE
∴AB=CE,
又∵ABCD为平行四边形,
∴AB=CD,
∴CE=CD,
∴△CDE为等腰三角形,
在等腰三角形CDE中,DE边上的高CM=OF=3,
∵DE=10-8=2,
∴由勾股定理得,CE2=OF2+(
 DE)2,
DE)2,∴CE=
 ,
,故答案为
 .
.本题考查了勾股定理和垂径定理以及平行四边形的性质,是基础知识要熟练掌握.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目

 cm
cm cm
cm  cm
cm ,圆心角等于45°的扇形
,圆心角等于45°的扇形 内部作一个正方形
内部作一个正方形 ,使点
,使点 在
在 上,点
上,点 在
在 上,点
上,点 在
在 上,则阴影部分的面积为(结果保留
上,则阴影部分的面积为(结果保留 ) .
) .

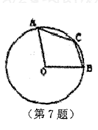
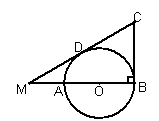
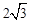 ,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为
,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为