题目内容
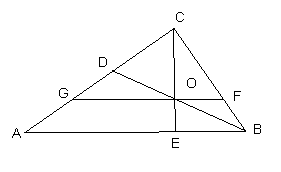
已知:如图,在⊿ABC中,∠ACB=90°,BD平分∠ABC,交AC于点D,CE⊥AB于点E,交BD于点O,过点O作FG∥AB,分别交BC、AC于点F、G.
求证:(1)⊿COD是等腰三角形;(2)CD=GA
 |
证明:(1)∵BD平分∠ABC,∴∠1=∠2,
∵∠BCD=90°,∴∠1+∠3=90°,∵CE⊥AB,
∴∠BEO=90°,∴∠2+∠4=90°∴∠3=∠4, ∵∠4=∠5,∴∠3=∠5
∴OC=OD,即⊿COD是等腰三角形 … 4分
(2)过点D作DH⊥AB于H
∵BD平分∠ABC,DH⊥AB于H,DC⊥BC于C,∴DC=DH,∵DC=OC, ∴OC=DH,
∵FG∥AB,∴∠6=∠A,∴⊿COG≌⊿DHA, ∴CG=DA, ∴CG-DG=DA-DG,即CG=AG. … 8分

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,