题目内容
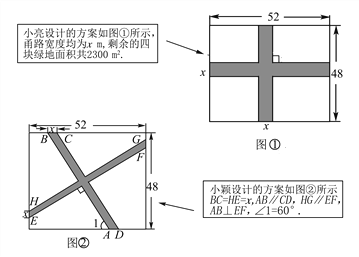
【题目】要在一块长52 m，宽48 m的矩形绿地上，修建同样宽的两条互相垂直的甬路，下面分别是小亮和小颖的设计方案．
(1)求小亮设计方案中甬路的宽度x；
(2)求小颖设计方案中四块绿地的总面积．(友情提示：小颖设计方案中的x与小亮设计方案中的x取值相同)
【答案】(1) 小亮设计方案中甬路的宽度为2m;(2) 2299m2.
【解析】试题分析：（1）利用平移把互相垂直的小路分别移到左侧和下面，表示出绿地的长和宽，建立绿地面积的一元二次方程求解；（2）由上题知道了甬路的宽，此题绿地面积应该等于矩形面积减去两个平行四边形的面积再加上两个平行四边形重合的小正方形的面积，因为两条甬路为平行四边形，所以求出平行四边形的高是解决问题的关键，过A点作CD边上的高，利用60度的正弦值求出高，即可求出绿地面积．
试题解析：（1）由题意可得，绿地的长为（52-x）m，绿地的宽为（48-x）m，因为绿地面积共2300平方米，所以列方程得：（52-x）（48-x）=2300，去括号得：x2-100x+196=0，解得：x1=2，x2=98（不合题意舍去），所以x=2，即甬路的宽度为2m；（2）过A点作AI⊥CD，HJ⊥EF，垂足分别为I，J，因为AB∥CD，∠1=60°，所以∠ADI=60°，因为BC∥AD，所以四边形ADCB为平行四边形，所以BC=AD，由上题得甬路x=2，所以BC=HE=2=AD，在Rt△ADI中，AI=2sin60°=
，所以绿地面积应该等于矩形面积减去两个平行四边形的面积再加上两个平行四边形重合的小正方形的面积，即为52×48-52×2-48×2+
=2496-104-96+3=2299（平方米）．
练习册系列答案
相关题目
