题目内容
【题目】如图,在![]() 中,
中,![]() 于
于![]() 点,
点,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() 并延长,交
并延长,交![]() 于
于![]() 点,
点,![]() .
.

(1)![]() 与
与![]() 有什么位置关系,说明理由;
有什么位置关系,说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的度数和
的度数和![]() 的长度;
的长度;
(3)在(2)的条件下,若将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,则(1)中结论是否仍然成立?如果成立,请证明;如果不成立,请直接写出此时
,则(1)中结论是否仍然成立?如果成立,请证明;如果不成立,请直接写出此时![]() 的度数.
的度数.
【答案】(1)![]() ,理由详见解析;(2)
,理由详见解析;(2)![]() ,
,![]() ;(3)不成立,
;(3)不成立,![]()
【解析】
(1)根据已知条件可证得![]() ,再根据全等三角形的性质即可得证结论
,再根据全等三角形的性质即可得证结论![]() ;
;
(2)根据等腰三角形的性质、三角形内角和定理可得出![]() ,再利用角的和差得
,再利用角的和差得![]() ,进而求得
,进而求得![]() ,然后根据等腰直角三角形的性质、含
,然后根据等腰直角三角形的性质、含![]() 角的直角三角形的性质以及勾股定理即可求得
角的直角三角形的性质以及勾股定理即可求得![]() ;
;
(3)画出旋转之后的图形,根据旋转的性质以及三角形的外角性质即可求得结论.
解:(1)结论:![]()
理由:∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() ;
;
(2)∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∵由(1)可知:![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵由(1)可知:![]() ,且
,且![]()
∴![]()
∴![]() ;
;
(3)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,如图:
,如图:

∴![]()
∴不成立,![]() .
.

练习册系列答案
相关题目
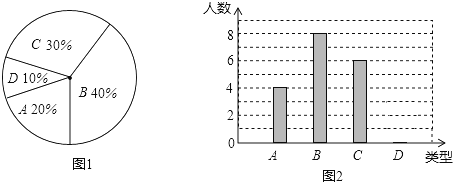
【题目】为了传承中国传统文化,某校组织了一次全体学生“汉字听写”大赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果作为样本进行整理,绘制成如下的统计图表:
组别 | 正确字数x | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |

根据以上信息完成下列问题:
(1)统计表中的![]() ________,
________,![]() ________,并补全条形统计图;扇形统计图中“C组“所对应的圆心角的度数是________;
________,并补全条形统计图;扇形统计图中“C组“所对应的圆心角的度数是________;
(2)已知该校共有600名学生,如果听写正确的字的个数不少于24个定为合格,请你估计该校本次听写比赛合格的学生人数.