题目内容
【题目】如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由.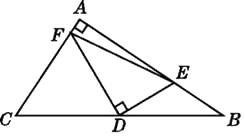
【答案】解:FC2+BE2=EF2.理由如下:
∵点D为BC的中点,∴BD=CD.作△BDE关于点D成中心对称的
△CDM,如图.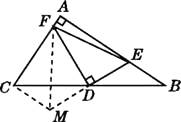
由中心对称的性质可得CM=BE,MD=ED,∠DCM=∠B.
又∵∠B+∠ACB=90°,
∴∠DCM+∠ACB=90°,即∠FCM=90°.
连接FM.在△FME中,MD=ED,FD⊥ME,FD=FD,
∴△FDM≌△FDE.∴FM=EF.
又∵在Rt△FCM中,FC2+CM2=FM2,
∴FC2+BE2=EF2.
【解析】根据点D为BC的中点,作△BDE关于点D成中心对称的△CDM,根据中心对称的性质得出CM=BE,MD=ED,∠DCM=∠B,再根据直角三角形的两锐角互余证得∠B+∠ACB=90°,从而证得△FCM是直角三角形,利用勾股定理得出,FC2+CM2=FM2,然后再证明FM=EF,即可证得结论。
【考点精析】掌握勾股定理的概念和中心对称及中心对称图形是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

