题目内容
【题目】△ABC是等腰直角三角形，BC=AC，直角顶点C在x轴上，一角顶点B在y轴上．
（1）如图①若AD⊥x轴，垂足为点D．点C坐标是（﹣1，0），点B的坐标是（0，2），求A点的坐标．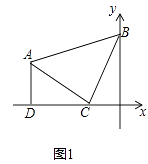
（2）如图②，直角边BC在两坐标轴上滑动，若y轴恰好平分∠ABC，AC与y轴交于点D，过点A作AE⊥y轴于E，求证：BD=2AE．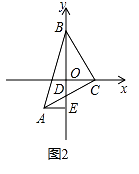
（3）如图③，直角边BC在两坐标轴上滑动，使点A在第四象限内，过A点作AF⊥y轴于F，在滑动的过程中，两个结论：① 
为定值；② 
为定值，只有一个结论成立，请你判断正确的结论并求出定值．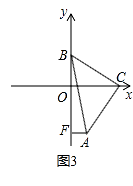
【答案】
（1）
解：∵∠ACB=90°，
∴∠ACD+∠BCO=90°，
∵AD⊥CD，
∴∠ACD+∠CAD=90°，
∴∠BCO=∠CAD，
在△ACD和△CBO中，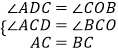 
，
∴△ACD≌△CBO，
∴AD=CO=1，DC=OB=2，
∴OD=OC+CD=3，
∴A（﹣3，1）
（2）
解：如图，
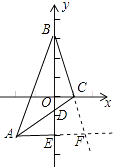
延长AE、BC交于点F，
∵y轴平分∠ABC，AE⊥y轴，
∴AE=EF，
∴AF=2AE，
∵AE⊥x轴，
∴∠EAD+∠ADE=90°，
∵∠ADE=∠BDC，
∴∠EAD+∠BDC=90°，
∵∠ABC=90°，
∴∠BDC+∠CBD=90°，
∴∠DAE=∠CBD，
在△BCD和△ACF中，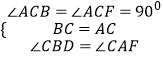 
，
∴△BCD≌△ACF，
∴BD=AF，
∵AF=2AE，
∴BD=2AE
（3）
解：① 
为定值，理由：
如图3，
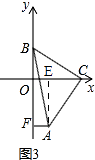
作AE⊥OC于E，
∵∠ACB=90°，
∴∠OCB+∠OCA=90°，
∵∠OBC+∠OCB=90°，
∴∠OCA=∠OBC，
在△OBC和△ECA中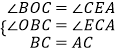 
．
∴△OBC≌△ECA，
∴OB=CE，
∵AF=OE
∴① = 
= 
=1是定值，
② 
= 
= 
= 
+ = +1，而2AF与AB的关系不知，
∴②不是定值．
即：① 为定值
【解析】（1）先判断出，∠BCO=∠CAD，从而得出△ACD≌△CBO，求出AD=CO=1，DC=OB=2即可；（2）先利用等腰三角形的判定得出AF=2AE，同（1）的方法判断出△BCD≌△ACF，得出BD=AF即可；（3）作AE⊥OC，同（1）方法判断出△OBC≌△ECA得出OB=CE，最后结合图形求出①个结论是定值．
【考点精析】通过灵活运用等腰三角形的性质，掌握等腰三角形的两个底角相等（简称：等边对等角）即可以解答此题．
