题目内容

一个三角形其中两个内角都小于40°，该三角形是


  1. A.
    直角三角形
  2. B.
    锐角三角形
  3. C.
    钝角三角形
  4. D.
    无法确定
C
分析：设三角形的三个角的度数分别是x°，y°，z°，不妨设x＜40，y＜40，根据三角形的内角和定理，即可确定．
解答：设三角形的三个角的度数分别是x°，y°，z°，不妨设x＜40，y＜40．
又∵x+y+z=180
∴z＞100．
则三角形一定是一个钝角三角形．
故选C．
点评：本题考查了三角形的内角和定理，关键是根据内角和定理确定内角的度数的范围．
练习册系列答案
相关题目
用剪刀将形状如图（甲）所示的矩形纸片ABCD沿着直线CM剪成两部分，其中M为AD的中点．用这两部分纸片可以拼成一些新图形，例如图（乙）中的Rt△BCE就是拼成的一个图形．
（1）用这两部分纸片除了可以拼成图乙中的Rt△BCE外，还可以拼成一些四边形．请你试一试，把拼好的四边形分别画在图丙、图丁的虚框内；
（2）若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形，设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米，且a、b恰好是关于x的方程x2-（m-1）x+m+1=0的两个实数根，试求出原矩形纸片的面积．
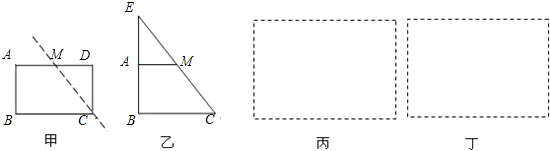
精英家教网
20、按要求解答下列问题：
（1）图1是一块直角三角形纸片，将该三角形纸片按如图方法折叠，使点A与点C重合，DE为折痕，试证明△CBE为等腰三角形；
（2）再将图1中的△CBE沿对称轴EF折叠（如图2）．通过折叠，原三角形恰好折成两个完全重合的矩形，其中一个是内接矩形，另一个是拼合（指无缝隙无重叠）所成的矩形，我们称这样的两个矩形为“组合矩形”，你能将图3中的△ABC折叠成一个组合矩形吗？如果能折成，请在图3中画出折痕；
（3）请你在图4的方格纸中画出一个斜三角形，使它同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点（各小正方形顶点）上．（画出一个即可）．
15、全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC和△A1B1C1是全等 合同．三角形，点A与点A1对应，点B与点B1对应，点C与点C1对应，当沿周界A→B→C→A，及A1→B1→A1环绕时，若运动方向相同，则称它们是真正合同三角形 如图，若运动方向相反，则称它们是镜面合同三角形 如图，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合，两个镜面合同三角形要重合，则必须将其中一个翻转180° 如图，下列各组合同三角形中，是镜面合同三角形的是（　　）
（2013•连云港）小明在一次数学兴趣小组活动中，对一个数学问题作如下探究：
问题情境：如图1，四边形ABCD中，AD∥BC，点E为DC边的中点，连接AE并延长交BC的延长线于点F，求证：S四边形ABCD=S△ABF（S表示面积）

问题迁移：如图2：在已知锐角∠AOB内有一个定点P．过点P任意作一条直线MN，分别交射线OA、OB于点M、N．小明将直线MN绕着点P旋转的过程中发现，△MON的面积存在最小值，请问当直线MN在什么位置时，△MON的面积最小，并说明理由．

实际应用：如图3，若在道路OA、OB之间有一村庄Q发生疫情，防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线，建立一个面积最小的三角形隔离区△MON．若测得∠AOB=66°，∠POB=30°，OP=4km，试求△MON的面积．（结果精确到0.1km2）（参考数据：sin66°≈0.91，tan66°≈2.25，
3
≈1.73）
拓展延伸：如图4，在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）（6，3）（
9
2
，
9
2
）、（4、2），过点p的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形面积的最大值．

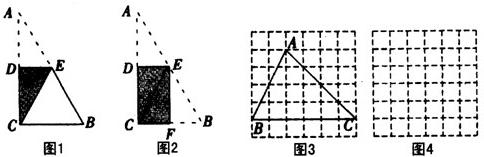
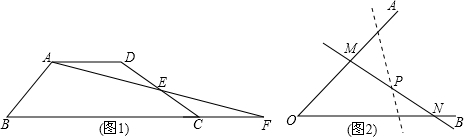
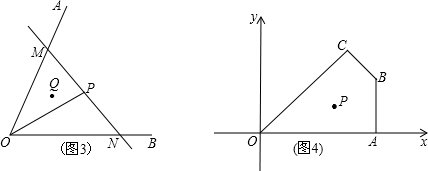
全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC和是全等(合同)三角形，且点A与点对应，点B与点对应，点C与点对应，当沿周界A→B→C→A及环绕时，若运动方向相同，则称它们是真正合同三角形(如下图)；若运动方向相反，则称它们是镜面合同三角形，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合，而两个镜面合同三角形要重合，则必须将其中的一个翻转180°．

下列选项的各组三角形中，是镜面三角形的是

[　　]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网