题目内容
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
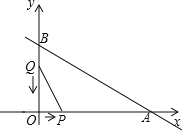
(1)设△POQ的面积为s,写出s关于t的函数关系式;当t为何值时,△POQ的面积最大,这时面积是多少
(2)当t为何值时,△POQ与△AOB相似?
【答案】(1)s=﹣![]() t2+3t,(0≤t≤6);t=3时,s有最大值
t2+3t,(0≤t≤6);t=3时,s有最大值![]() .(2)当t=4或t=2时,△POQ与△AOB相似.
.(2)当t=4或t=2时,△POQ与△AOB相似.
【解析】
试题分析:(1)直接根据三角形的面积公式即可得出结论;
(2)分△POQ∽△AOB与△POQ∽△BOA两种情况进行讨论.
解:(1)∵OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动,
∴OB=6﹣t,OP=t,
∴s=OQOP=![]() (6﹣t)t=﹣
(6﹣t)t=﹣![]() t2+3t,(0≤t≤6)
t2+3t,(0≤t≤6)
配方得,s=﹣![]() t2+3t=﹣
t2+3t=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,
,
因为﹣![]() <0,所以,当t=3时,s有最大值
<0,所以,当t=3时,s有最大值![]() .
.
(2)①若△POQ∽△AOB时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
整理得,12﹣2t=t,解得,t=4;
②若△POQ∽△BOA时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
整理得:6﹣t=2t,解得:t=2.
∵0≤t≤6,
∴t=4和t=2均符合题意,
∴当t=4或t=2时,△POQ与△AOB相似.

练习册系列答案
相关题目

