题目内容
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,E是AB上一点,连接CE,现将
,E是AB上一点,连接CE,现将![]() 向上方翻折,折痕为CE,使点B落在点P处.
向上方翻折,折痕为CE,使点B落在点P处.

(1)当点P落在CD上时,![]() _____;当点P在矩形内部时,BE的取值范围是_____.
_____;当点P在矩形内部时,BE的取值范围是_____.
(2)当点E与点A重合时:①画出翻折后的图形(尺规作图,保留作图痕迹);②连接PD,求证:![]() ;
;

(3)如图,当点Р在矩形ABCD的对角线上时,求BE的长.

【答案】(1)12,0<BE<12;(2)①见解析,②见解析;(3)6或9.
【解析】
(1)由折叠的性质得到推出△BCE是等腰直角三角形,即可得到结论;
(2)①由题意画出图形即可;
②根据全等三角形的性质得到∠PAC=∠DCA,设AP与CD相交于O,于是得到OA=OC,求得∠OAC=∠OPD,根据平行线的判定定理得到结论;
(3)分两种情形,当点P在对角线AC或对角线BD上时,两种情形分别求解即可.
解:(1)当点P在CD上时,如图1,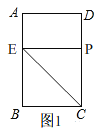
∵将∠B向右上方翻折,折痕为CE,使点B落在点P处,
∴∠BCE=∠ECP=45°,
∴△BCE是等腰直角三角形,
∴BE=BC=AD=12,
当点P在矩形内部时,BE的取值范围是0<BE<12;
故答案为:12,0<BE<12;
(2)①补全图形如图2所示,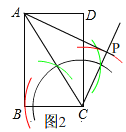
②当点E与点A重合时,如图3,连接PD,设CD交PA于点O.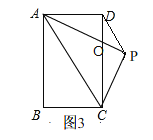
由折叠得,AB=AP=CD,
在△ADC与△CPA中,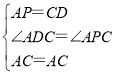 ,
,
∴△ADC≌△CPA,
∴∠PAC=∠DCA,
设AP与CD相交于O,则OA=OC,
∴OD=OP,∠ODP=∠OPD,
∵∠AOC=∠DOP,
∴∠OAC=∠OPD
∴PD∥AC;
(3)如图4中,当点P落在对角线AC上时,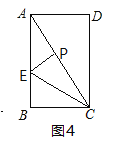
由折叠得,BC=PC=12,AC=![]() =20,
=20,
∴PA=8,设BE=PE=x,
在Rt△APE中,(16-x)2=x2+82,
解得x=6.
∴BE=6.
如图5中,当点P落在对角线BD上时,设BD交CE于点M.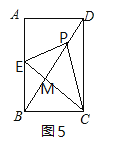
由折叠得,BE=PE,∠BEC=∠PEC,
∵EM=EM,
∴△MBE∽△MEP,
∴∠EMB=∠EMP,
∵∠EMB+∠EMP=180°,
∴EC⊥BD,
∴∠BCE=∠ABD,
∵∠A=∠ABC=90°,
∴△CBE∽△BAD,
∴![]() ,
,
∴![]() ,
,
∴BE=9,
综上所述,满足条件的BE的值为6或9.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.