题目内容
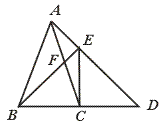
如图，在△ABC中，AB＝AC，延长BC至D，使得CD＝BC，CE⊥BD交AD于E，连结BE交AC于F，求证AF＝FC．
【提示】先证△BCF∽△DBA，再证
＝
．
【答案】∵ BC＝CD，EC⊥BD，
∴ BE＝DE，∠FBC＝∠D．
又 AB＝AC，
∴ ∠BCF＝∠DBA．
∴ ∠BCF∽△DBA．
∴ 
＝
．
又 BD＝2BC，AB＝AC，
∴ ＝
＝．
∴ FC＝AC．
因此 AF＝FC．
练习册系列答案
字词句段篇系列答案
相关题目
字词句段篇系列答案
20、如图，在△ABC中，∠BAC=45°，现将△ABC绕点A逆时针旋转30°至△ADE的位置，使AC⊥DE，则∠B=
如图，在△ABC中，∠ACB=90°，AC=BC=1，取斜边的中点，向斜边作垂线，画出一个新的等腰三角形，如此继续下去，直到所画出的直角三角形的斜边与△ABC的BC重叠，这时这个三角形的斜边为
2、如图，在△ABC中，DE∥BC，那么图中与∠1相等的角是（ ）
如图，在△ABC中，AB=AC，且∠A=100°，∠B=