题目内容
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为 . 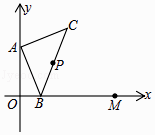
【答案】![]()
【解析】解:如图所示,过P作PD⊥x轴于D,作PE⊥y轴于E,则∠DPE=90°,∠AEP=∠BDP=90°,
连接AP,
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP= ![]() BC=BP,且AP⊥BC,即∠APB=90°,
BC=BP,且AP⊥BC,即∠APB=90°,
∴∠APE=∠BPD,
在△AEP和△BDP中, ,
,
∴△AEP≌△BDP(AAS),
∴PE=PD,
∴点P的运动路径是∠AOM的角平分线,
如图所示,当点B与点O重合时,AB=AO=1,OC= ![]() ,
,
∴OP= ![]() OC=
OC= ![]() ;
;
如图所示,当点B与点M重合时,过P作PD⊥x轴于D,作PE⊥y轴于E,连接OP,
由△AEP≌△BDP,可得AE=BD,
设AE=BD=x,则OE=1+x,OD=2﹣x,
∵矩形ODPE中,PE=PD,
∴四边形ODPE是正方形,
∴OD=OE,即2﹣x=1+x,
解得x= ![]() ,
,
∴OD=2﹣ ![]() =
= ![]() ,
,
∴等腰Rt△OPD中,OP= ![]() OD=
OD= ![]() ,
,
∴当点B从点O向x轴正半轴移动到点M时,则点P移动的路线长为 ![]() ﹣
﹣ ![]() =
= ![]() .
.
故答案为: ![]() .
.
先过P作PD⊥x轴于D,作PE⊥y轴于E,根据△AEP≌△BDP(AAS),得出PE=PD,进而得到点P的运动路径是∠AOM的角平分线,再分别求得当点B与点O重合时,OP= ![]() OC=
OC= ![]() ,当点B与点M重合时,OP=
,当点B与点M重合时,OP= ![]() OD=
OD= ![]() ,进而得到点P移动的路线长.
,进而得到点P移动的路线长.

练习册系列答案
相关题目


