题目内容
7、在△ABC中，AC=CD且∠CAB-∠B=30°，则∠BAD=15°
．分析：从已知条件开始思考，根据三角形内角与外角之间的关系列方程解答即可．
解答：解：设∠BAD=x，则∠CDA=∠x+∠B，
∵AC=CD，
∴∠CAD=∠CDA=x+∠B，
于是∠CAB=∠2x+∠B，
又∠CAB-∠B=30°，
∴2x+∠B-∠B=30°，
解得x=15°．
故答案为15°．
∵AC=CD，
∴∠CAD=∠CDA=x+∠B，
于是∠CAB=∠2x+∠B，
又∠CAB-∠B=30°，
∴2x+∠B-∠B=30°，
解得x=15°．
故答案为15°．
点评：本题考查了等腰三角形的性质；在求角的度数时，若不易求出，常用设未知数列方程的方法求解，这是一种很重要的方法要注意掌握．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，AC=8，BC=6，AB=10，则△ABC的外接圆半径长为（ ）
| A、10 | B、5 | C、6 | D、4 |
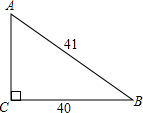如图，在△ABC中，AC=
如图所示，在△ABC中，AC与⊙O相切于点A，AC=AB=2，⊙O交BC于D．
（2013•松江区二模）如图，已知在△ABC中，AC=15，AB=25，sin∠CAB=