Question

【题目】已知抛物线（其中、为常数且）与轴交于和两点，与轴交于点.

（1）当时，求抛物线的对称轴方程及顶点坐标；

（2）填空：__________，点的坐标为____________.（以上结果均用含的式子表示）；

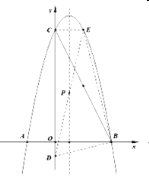
（3）连接，线段的垂直平分线交抛物线的对称轴于点，轴上存在一点（异于点）使得.

①求点的坐标；

②点关于抛物线对称轴的对称点为点，试求面积的最大值.

Answer 1

【答案】（1），；（2），；（3）①，②37

【解析】

（1）代入，根据过可求出n，然后将解析式化成顶点式可得对称轴方程及顶点坐标；

（2）代入，整理可得，然后根据抛物线的对称性求点的坐标；

（3）①求出点C坐标，设，，分别根据和利用两点间距离公式列出方程求解即可；

②根据列式化简，然后利用二次函数的性质求最大值即可.

（1）当时，抛物线的解析式为，

代入得：，

解得，

即解析式为，

∴抛物线的对称轴为：，顶点坐标为；

（2）依题意得，，则，

∵抛物线的对称轴为：，由对称性可得；

（3）①依题意，得，即，设，

∵在线段的垂直平分线上，

∴，

∴，

∴，

解得：，即，

设，

∴，

∴，

∴，

解得，，（舍），

∴；

②，

，

，

，

当时，面积随的增大而增大，

∴当时，面积的最大值为.